Geometrijski red
Ovaj članak ili neki od njegovih odlomaka nije dovoljno potkrijepljen izvorima (literatura, veb-sajtovi ili drugi izvori). |
- Ovo je članak o beskonačnom geometrijskom redu. Za članak o konačnoj sumi, pogledajte geometrijska progresija.

U matematici, geometrijski red je red sa konstantnim omjerom između susjednih članova. Na primjer, red
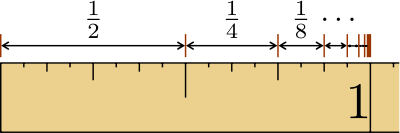
je geometrijski, zato što je svaki član jednak polovini svog prethodnog člana. Suma ovog reda je 1, kao što je prikazano na slijedećoj slici:
Geometrijski redovi su najjednostavniji primjeri beskonačnih redova sa konačnim sumama. To ih čini važnim za filozofiju, gdje oni nude matematičko rješenje za Zenonove paradokse. Historijski, geometrijski redovi igrali su važnu ulogu u ranom razvitku kalkulusa, te su još važni za proučavanje konvergencije redova. Geometrijski redovi se koriste u cijeloj matematici, a imaju važne primjene u fizici, inženjerstvu, biologiji, ekonomiji i finansijama.
Zajednički omjer[uredi | uredi izvor]
Članovi geometrijskog reda dolaze iz geometrijske progresije, što znači da je omjer susjednič članova konstantan. Slijedeća tabela prikazuje nekoliko geometrijskih redova sa tazličitim omjerom:
| Zajednički omjer | Primjer |
|---|---|
| 10 | 4 + 40 + 400 + 4000 + 40,000 + ··· |
| 1/3 | 9 + 3 + 1 + 1/3 + 1/9 + ··· |
| 1/10 | 7 + 0.7 + 0.07 + 0.007 + 0.0007 + ··· |
| 1 | 3 + 3 + 3 + 3 + 3 + ··· |
| –1/2 | 1 – 1/2 + 1/4 – 1/8 + 1/16 – 1/32 + ··· |
| –1 | 3 – 3 + 3 – 3 + 3 – ··· |
Ponašanje članova zavisi od zajedničkog omjera r:
- Kada je r veće od jedan, članovi reda postaju veći i veći.
- Kada je r manje od jedan (i veći od nula), članovi reda postaju sve manji i manji, te teže nuli kao svojoj graničnoj vrijednosti (limes).
- Kada je r jednako jedan, svi članovi reda su isti.
Zajednički omjer može biti i negativan, što uzrokuje da znak ispred članovu alternira (znak je naizmjenično + ili -).
Suma[uredi | uredi izvor]
Suma geometrijskog reda je konačna sve dok članovi reda teže nuli. Suma se može izračunati koristeći samosličnost reda.
Primjer[uredi | uredi izvor]

Razmatrajmo sumu slijedećeg geometrijskog reda:
Ovaj red ima zajednički omjer od 2/3. Ako pomnožimo cijeli red sa ovim brojem, tada početni, koji je imao vrijednost 1, dobija vrijednost 2/3, 2/3 postaje 4/9, i tako dalje:
Ovaj novi red je isti kao i original, osim što prvi član nedostaje. Oduzimanjem ova dva reda poništavaju se svi članovi osim prvog:
Slična tehnika može se koristiti kod računanja bilo kojeg samosličnog izraza.
Formula[uredi | uredi izvor]
Suma prvih članova geometrijskog reda je:
- ( različito od 1).
gdje je a prvi član reda, a r je zajednički omjer.
Kada teži u beskonačnost, apsolutna vrijednost od mora biti manja od jedan kako bi red konvergirao. Suma tada postaje
- .
Kada je a = 1, izraz se pojednostavljuje u:
- ,
gdje je lijeva strana geometrijski red sa zajedničkim mjerom r. Možemo dobiti ovu formuli koristeći metod opisan u gornjem tesktu:
Opća formula slijedi ako sve pomnožimo sa a.
Ova formula važi za konvergentne redove (tj. kada je vrijednost r manja od jedan). Na primjer, suma nije definisana kada je r = 10, iako dobijamo rješenje s = –1/9.
Ovo pravilo, također, vrijedi, uz iste restrikcije, i za kompleksne brojeve.
Dokaz konvergencije[uredi | uredi izvor]
Možemo dokazati da geometrijski red konvergira koristeći formulu za sumu za geometrijsku progresiju:
Pošto je rn+1 → 0 za | r | < 1, limes iznosi 1 / (1 – r).
Primjene[uredi | uredi izvor]
Periodične decimale[uredi | uredi izvor]
Periodična decimala može se smatrati geometrijskim redom čiji je zajednički omjer je stepe na 1/10. Na primjer:
Možemo koristiti ovu formulu za sumiranje geometrijskog reda kako bi prikazali decimale u obliku razlomaka:
Arhimedova kvadratura parabole[uredi | uredi izvor]

Arhimed je koristi sumu geometrijskom reda kako bi izračunao površinu koju zatvaraju parabola i jedna prava linija. Njegov metod je bio da podijeli povšinu u beskonačan broj trouglova, kao što je prikazano na slici desno.
Arhimedov teorem: Ukupna površina ispod parabole je 4/3 površine planog trougla.
Dokaz: Koristeći znanje iz geometrije, Arhimed je odredio da svaki zeleni trougao ima 1/8 površine plavog trougla, da svaki žuti trougao ima 1/8 površine zelenog trougla, i tako dalje.
Pretpostavljajući za plani trougao ima površinu 1, ukupna površina je beskonačna suma:
Prvi član predstavlja površinu planog trougla, drugi član predstavlja površinu dva zelena trougla, treći član predstavlja površinu četiri žuta trougla, i tako dalje. Pojednostavljenjem razlomaka dobijamo
Ovo je geometrijski red sa zajedničkim omjerom 1/4. Suma iznosi
- Q.E.D.
Ovaj proračun koristi metod iscrpljenja, rana verzija integracije. U modernom kalkulusu, ista površina bi se mogla izračunati korištenjem određenog integrala.
Geometrija fraktala[uredi | uredi izvor]

U proučavanju fraktala, geometrijski red se često pojavljuje kao obim, površina ili zapremina samoslične figure.
Na primjer, površina unutar Kochove pahuljice može se opisati kao unija beskonačno mnogo jednakostraničnih trouglova (pogledajte sliku). Svaka stranica zelenog trougla je tačno 1/3 veličine stranice velikog planog trougla, tako da ima tačno 1/9 površine. Slično tome, svaki žuti trougao ima 1/9 površine zelenog trougla, i tako dalje. Uzimajući plani trougao za jediničnu površinu, ukupna površina pahuljice je
Prvi član reda predstavlja površinu plavog trougla, drugi član je ukupna površina tri zelena trougla, treći član je ukupna površina dvanaest žutih trouglova, i tako dalje. Isključujući početni član 1, ovaj red je geometrijski sa zajedničkim omjerom r = 4/9. Prvi član geometrijskog reda je a = 3(1/9) = 1/3, tako da je suma
Tako da Kochova pahulja ima 8/5 površine najvećeg (glavnog) trougla.
Zenonovi paradoksi[uredi | uredi izvor]
Razumijevanje konvergencije geometrijskog reda dozvoljava nam da riješimo mnoge Zenonove paradokse, pošto postoji pravilo da suma beskonačnog skupa može biti konačna ako vrijedi | r | < 1. Na primjer, Zenonova dihotomija iskazuje da je kretanje nemogće, pošto se put može podijeliti na korake polovine dužine preostale razdaljine, tako da je potreban beskonačan broj koraka da se pređe neka konačna daljina. Skrivena pretpostavka je ta da je suma beskonačnog broja konačnih koraka ne može biti konačna. Ovo, naravno, nije tačno kao što je i vidljivo po konvergenciji geometrijskog reda sa r=1/2, prikazanog na slici na početku ovog članka.
Ekonomija[uredi | uredi izvor]
U ekonomiji, geometrijski redovi se koriste za prikazivanje trenutne vrijednosti anuiteta (suma novca koji se treba isplatiti u pravilnim intervalima).
Geometrijski potencijalni red[uredi | uredi izvor]
Ovaj odlomak potrebno je proširiti. |
Također pogledajte[uredi | uredi izvor]
- Red (matematika)
- Geometrijska progresija
- D'Alambertov test
- Cauchyjev korjeni test
- Divergentni geometrijski red
- Neumannov red
Specifični geometrijski redovi[uredi | uredi izvor]
- Grandijev red
- 1 + 2 + 4 + 8 + · · ·
- 1 − 2 + 4 − 8 + · · ·
- 1/2 + 1/4 + 1/8 + 1/16 + · · ·
- 1/2 − 1/4 + 1/8 − 1/16 + · · ·
- 1/4 + 1/16 + 1/64 + 1/256 + · · ·
Reference[uredi | uredi izvor]
- James Stewart (2002). Calculus, 5th ed., Brooks Cole. ISBN 978-0-534-39339-7
- Larson, Hostetler, and Edwards (2005). Calculus with Analytic Geometry, 8th ed., Houghton Mifflin Company. ISBN 978-0-618-50298-1
- Roger B. Nelson (1997). Proofs without Words: Exercises in Visual Thinking, The Mathematical Association of America. ISBN 978-0-88385-700-7
- Andrews, George E. (1998). "The geometric series in calculus". The American Mathematical Monthly. 105 (1): 36–40. doi:10.2307/2589524.
Historija i filozifija[uredi | uredi izvor]
- C. H. Edwards, Jr. (1994). The Historical Development of the Calculus, 3rd ed., Springer. ISBN 978-0-387-94313-8.
- Swain, Gordon and Thomas Dence (1998). "Archimedes' Quadrature of the Parabola Revisited". Mathematics Magazine. 71 (2): 123–30. Nepoznati parametar
|month=zanemaren (pomoć) - Eli Maor (1991). To Infinity and Beyond: A Cultural History of the Infinite, Princeton University Press. ISBN 978-0-691-02511-7
- Morr Lazerowitz (2000). The Structure of Metaphysics (International Library of Philosophy), Routledge. ISBN 978-0-415-22526-7
Ekonomija[uredi | uredi izvor]
- Carl P. Simon and Lawrence Blume (1994). Mathematics for Economists, W. W. Norton & Company. ISBN 978-0-393-95733-4
- Mike Rosser (2003). Basic Mathematics for Economists, 2nd ed., Routledge. ISBN 978-0-415-26784-7
Biologija[uredi | uredi izvor]
- Edward Batschelet (1992). Introduction to Mathematics for Life Scientists, 3rd ed., Springer. ISBN 978-0-387-09648-3
- Richard F. Burton (1998). Biology by Numbers: An Encouragement to Quantitative Thinking, Cambridge University Press. ISBN 978-0-521-57698-7
Računarstvo[uredi | uredi izvor]
- John Rast Hubbard (2000). Schaum's Outline of Theory and Problems of Data Structures With Java, McGraw-Hill. ISBN 978-0-07-137870-3
Vanjski linkovi[uredi | uredi izvor]
- Peppard, Kim. "College Algebra Tutorial on Geometric Sequences and Series". West Texas A&M University.
- Casselman, Bill. "A Geometric Interpretation of the Geometric Series". Arhivirano s originala (Applet), 29. 9. 2007. Pristupljeno 6. 11. 2008.
- "Geometric Series" by Michael Schreiber, The Wolfram Demonstrations Project, 2007.










![{\displaystyle {\begin{array}{l}{\text{Neka je }}s\;=\;1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots .\\[4pt]{\text{Tada je }}rs\;=\;r\,+\,r^{2}\,+\,r^{3}\,+\,r^{4}\,+\,\cdots .\\[4pt]{\text{Tada je }}s\,-\,rs\;=\;1,\;\;\;\;{\mbox{tako da vrijedi }}s\,=\,{\frac {1}{1-r}}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78d97d65fcb1c6501241fb3895b463d2f918f826)
![{\displaystyle {\begin{aligned}&1\,+\,r\,+\,r^{2}\,+\,r^{3}\,+\,\cdots \\[3pt]&=\;\lim _{n\rightarrow \infty }\left(1\,+\,r\,+\,r^{2}\,+\,\cdots \,+\,r^{n}\right)\\&=\;\lim _{n\rightarrow \infty }{\frac {1-r^{n+1}}{1-r}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/515bf1c73549c67b4b2446dfe97f59df559018f9)






