Versinus i haversinus
Versinus ili obrnuti sinus je trigonometrijska funkcija koja se pojavljivala tokom ranog razvoja trigonometrije. Postoji još nekoliko srodnih funkcija i to coversinus i haversinus. Haversinus, koji predstavlja polovinu versinusa, ima izrazitu važnost kod haversinusne formule koja se koristi za navigaciju.

Pregled[uredi | uredi izvor]
Versinus[1][2][3][4][5] ili obrnuti sinus[3][6][7][8][9] je trigonometrijska funkcija koja se pojavljivala u najranijim trigonometrijskim tablicama. Piše se kao versin(θ),[3][7][8] sinver(θ),[10][11] vers(θ),[1][2][3][4][5][6] ver(θ)[12] ili siv(θ).[13][14] Na latinskom, ova funkcija je poznata kao sinus versus[13][14] (obrnuti sinus), versinus, versus ili sagitta (strijela).
Ova funkcija se može izraziti preko prave sinusne (t.j. "vertikalne" sinusne (sinus rectus)) i kosinusne (cosinus rectus) funkcije u obliku:
Postoji nekoliko srodnih funkcija koje odgovaraju versinusu i to:
- Obrnuti kosinus,[15] ili vercosinus,[15] koji se zapisuje kao vercosin(θ), vercos(θ)[15] ili vcs(θ)[12]
- Koverzirani sinus, coversinus,[2][4][5][7][8][16] naspramni kosinus[13][14], koji se zapisuje kao coversin(θ),[17]covers(θ),[2][4][5][6][11][16][18][19][20] cosiv(θ)[13][14] or cvs(θ)[8][11][12][21]
- Koverzirani kosinus[22] ili covercosinus,[22] koji se zapisuje kao covercosin(θ) or covercos(θ)[22] or cvc(θ)[12]
Analogno prethodnim funkcijama, postoje i još četiri funkcije iz kojih se dobija "polovična" vrijednost odgovarajuće "pune" vrijednosti neke od prethodnih funkcija:
- Haverzirani sinus,[23] haversinus[1][2][4][5][6][7][23] ili semiversus,[24][25] koji se zapisuje kao haversin(θ), semiversin(θ), semiversinus(θ), havers(θ),[1] hav(θ),[1][2][4][5][6][11][12][23][26][27] hvs(θ), sem(θ)[25] ili hv(θ),[28]. Ova funkcija se najčešće koristi u haversinusnoj formuli.
- Haverzirani kosinus[29] ili havercosinus,[29] koji se zapisuje kao havercosin(θ), havercos(θ),[29] hac(θ) ili hvc(θ)[12]
- Hakoverzirani sinus,[17] hacoversinus[17] ili kohaversinus[17] koji se zapisuje kao hacoversin(θ),[17] semicoversin(θ), hacovers(θ), hacov(θ)[30] or hcv(θ)[12]
- Hakoverzirani kosinus,[31] hakoverkosinus[31] or kohavercosinus[31] koji se zapisuje kao hacovercosin(θ), hacovercos(θ)[31] or hcc(θ)[12]
Historija i primjene[uredi | uredi izvor]
Versinus i koversinus[uredi | uredi izvor]

Obična sinusna funkcija se nekada historijski zvala sinus rectus ("vertikalni sinus"),kako bi se razlikovala od obrnutog sinusa (sinus versus).[32] Značenje ovih termina je očigledno kada se te funkcije posmatraju u okviru jedinične kružnice, pomoću koje su i definirane:
Za vertikalnu tetivu AB neke jedinične kružnice sinus ugla θ (koji je polovina naspramnog ugla Δ) je udaljenost AC (polovina tetive). Što se tiče obrnutog sinusa tog ugla θ, on predstavlja udaljenost CD od centra tetive do centra luka. Zbog ovoga, suma kosinusa tog ugla (koji je jednak dužini odsječka OC) i versinusa tog ugla θ je u stvari poliprečnik OD, dužine 1 jer se radi o jediničnoj kružnici. Ovako prikazano, sinus je vertikalan (odatle dolazi latinska riječ rectus, što doslovno znači "pravo") dok je versinus horizontalan (odatle dolazi latinska riječ versus, što doslovno znači "okrenuto, obrnuto").
Na slici je također ilustriran i razlog zbog kojeg se versinus nekada zove sagitta, (lat. strijela),[33] ili na arapskom sahem[34] što ima isto značenje. Ako se kružni odsječak ADB, kojeg stvara ugao Δ i koji je jednak 2θ, posmatra kao luk za odapinjanje strijele a tetiva AB kao njegova "struna", onda se versinus CD jasno vidi kao "drška od strijele".
Uz navedenu interpretaciju običnog sinusa kao "vertikalnog" i obrnutog sinusa kao "horizontalnog", može se zaključiti da je sagitta u stvari zastarjeli sinonim za apscisu (horizontalnu osu grafa).[33]
1821 godine, Cauchy je koristio termine sinus versus (siv) za versinus i cosinus versus (cosiv) za coversinus.[13][14]

Historijski, obrnuti sinus je bio jedna od najvažnijih trigonometrijskih funkcija.[9][32][34]
Haversinus[uredi | uredi izvor]
Haversinus, je bio veoma bitan kod navigacije, jer se koristio u haversinusnoj formuli, koja se koristila kako bi se precizno izračunale udaljenosti u astronomiji kada bi bile poznate ugaone pozicije (npr., longituda i latituda).
1835 godine, termin haversinus (eng. haversine) (označavano kao log. haversine, log. havers. i hav.) je prvi put koristio[35] James Inman[11][36][37] u trećem izdanju njegovog rada "Navigation and Nautical Astronomy: For the Use of British Seamen" kako bi se pojednostavili proračuni udaljenosti između dvije tačke na površini Zemlje, korištenjem sferne trigonometrije u navigaciji.[1][35] Inman je također koristio termine nat. versinus i nat. vers. za versinuse.[1]
Druge bitne tablice haversinusa su napravljene od strane Richarda Farleya 1856 godine[38][39] i Johna Caulfielda Hannyngtona 1876 godine.[38][40]
Moderne primjene[uredi | uredi izvor]
Iako se primjena haversinusa i zadržala u navigaciji, ova trigonometrijska funkcija je pronašla i nove primjene u prethodnim decenijama, kao npr. kod Bruce D. Starkovog metoda koji se koristi kod preciziranja lunarnih udaljenosti korištenjem Gausovih logaritama[41][42] ili u kompaktnijoj metodi za redukciju vidljivosti (također u navigaciji).[28]
Jedan period (0 < θ < ) versinusne ili, češće, haversinuse (ili havercosinuse) talasne forme je također često korišten kod obrade signala i teorije upravljanja kod analize pulsa, zbog toga što postoji gladak prelaz (kontinualan u vrijednosti i nagibu) između nule i jedinice (za haversinus) i nakon toga ponovo u nulu. U ovakvoj primjeni, naziva se Hannova funkcija ili uzdignuti-kosninusni filter. Isto tako, havercosinus se koristi kod uzdignutih-kosinusnih distribucija u teoriji vjerovatnoće i statistici.
U formi sin2(θ) haversinus dvostrukog ugla Δ opisuje relaciju između udaljenosti stranica i uglova u racionalnoj trigonometriji, u predloženoj reformulaciji metričkih ravni i geometrije krutih objekata od strane Normana John Wildberger.[43]
Varijante haversinusa i haverkosinusa sa dvostrukim uglovima Δ (lat. sagitta i cosagitta) su također pronašle nove primjene u opisu korelacije i antikorelacije koreliranih fotona u kvantnoj mehanici.[44]
Matematički identiteti[uredi | uredi izvor]
Definicije funkcija[uredi | uredi izvor]
| [2][3][4][5][6][7][8][13][14] | 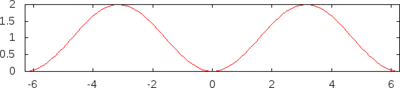
|
| [15] | 
|
| [2][4][5][6][8][11][13][14][16][18][19][20][21] | 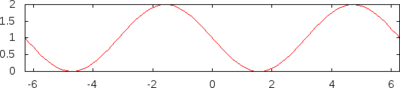
|
| [22] | 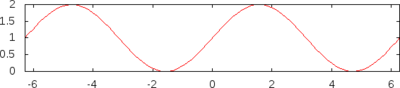
|
| [2][4][5][6][23] | 
|
| [29] | 
|
| [17] | 
|
| [31] | 
|
Izvodi i integrali[uredi | uredi izvor]
| [3] | [2][3] |
| [16] | [16] |
| [23] | [23] |
Inverzne funkcije[uredi | uredi izvor]
Za prethodno navedene trigonometrijske funkcije postoje i odgovarajuće inverzne funkcije:
Druge osobine[uredi | uredi izvor]
Ove funkcije se mogu proširiti i na kompleksnu ravan.[3][16][23]
Maclaurinov red za versinus i haversinus je definiran na sljedeći način:
Aproksimacije[uredi | uredi izvor]


Kada je versinus v manji u poređenju sa poluprečnikom r, on može biti aproksimiran dužinom polovične tetive L preko relacije:
- .[52]
Alternativno, ako je versinus mali i ako su vrijednosti versinusa, poluprečnika, i dužine polovične tetive poznate, one se mogu koristiti za estimaciju lučne dužine s (AD u slici iznad) korištenjem:
Ova formula je bila poznata kineskom matematičaru Shen Kuou, dok je nakon dva vijeka bila izvedena tačnija formula koja uključuje sagittu od strane drugog kineskog matematičara Guo Shoujinga.[53]
Još tačnija formula za aproksimaciju koja se koristi u inženjerstvu[54] je data kao:
Proizvoljne krive i tetive[uredi | uredi izvor]
Termin versinus je također nekada korišten za opis devijacija od nekog pravca kod proizvoljne krive na nekoj ravni, od čega iznad navedeni krug predstavlja specijalan slučaj. Ako je dana tetiva, koja spaja neke dvije tačke na krivoj, okomita udaljenost v od tetive do krive (u tački koja je u većini slučaja tačka na središtu tetive) se naziva versinusna mjera. Za pravu liniju, versinus bilo koje tetive je nula, zbog čega ova mjera i jeste karakteristika "pravosti" krive. Kod limesa kako se dužina tetive L približava nuli, omjer se sve više približava trenutačnoj zakrivljenosti. Ova primjena je veoma bitna u željezničkom prometu, gdje opisuje mjeru "pravosti" željezničkih pruga[55] i prestavlja osnovu za Halladeov method za mjerenje pruga.
Term sagitta je na sličan način korišten u optici prilikom opisivanja površina leća i ogledala.
Također pogledajte[uredi | uredi izvor]
- Trigonometrijske funkcije
- Exsekans i exkosekans
- Versiera
- Eksponencijalne funkcije
- Logaritamske funkcije
Reference[uredi | uredi izvor]
- ^ a b c d e f g Inman, James (1835) [1821]. Navigation and Nautical Astronomy: For the Use of British Seamen (3 izd.). London, UK: W. Woodward, C. & J. Rivington. Pristupljeno 9. 11. 2015. (Fourth edition: [1].)
- ^ a b c d e f g h i j Zucker, Ruth (1983) [June 1964]. "4.3.147: Elementary Transcendental Functions - Circular functions". u Abramowitz, Milton; Stegun, Irene Ann (ured.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first izd.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. str. 78. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. 6512253.
- ^ a b c d e f g h Weisstein, Eric W. "Versine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 31. 3. 2010. Pristupljeno 5. 11. 2015.
- ^ a b c d e f g h i Tapson, Frank (2004). "Background Notes on Measures: Angles". 1.4. Cleave Books. Arhivirano s originala, 9. 2. 2007. Pristupljeno 12. 11. 2015.
- ^ a b c d e f g h i Oldham, Keith B.; Myland, Jan C.; Spanier, Jerome (2009) [1987]. "32.13. The Cosine cos(x) and Sine sin(x) functions - Cognate functions". An Atlas of Functions: with Equator, the Atlas Function Calculator (2 izd.). Springer Science+Business Media, LLC. str. 322. doi:10.1007/978-0-387-48807-3. ISBN 978-0-387-48806-6. LCCN 2008937525.
- ^ a b c d e f g h Korn, Grandino Arthur; Korn, Theresa M. (2000) [1961]. "Appendix B: B9. Plane and Spherical Trigonometry: Formulas Expressed in Terms of the Haversine Function". Mathematical handbook for scientists and engineers: Definitions, theorems, and formulars for reference and review (3 izd.). Mineola, New York, USA: Dover Publications, Inc. str. 892–893. ISBN 978-0-486-41147-7. (See errata.)
- ^ a b c d e Boyer, Carl Benjamin (1969) [1959]. "5: Commentary on the Paper of E. J. Dijksterhuis (The Origins of Classical Mechanics from Aristotle to Newton)". u Clagett, Marshall (ured.). Critical Problems in the History of Science (3 izd.). Madison, Milwaukee, and London: University of Wisconsin Press, Ltd. str. 185–190. ISBN 0-299-01874-1. LCCN 59-5304. 9780299018740. Pristupljeno 16. 11. 2015.
- ^ a b c d e f Swanson, Todd; Andersen, Janet; Keeley, Robert (1999). "5 (Trigonometric Functions)". Precalculus: A Study of Functions and Their Applications (PDF). Harcourt Brace & Company. str. 344. Arhivirano s originala (PDF), 17. 6. 2003. Pristupljeno 12. 11. 2015.
- ^ a b Calvert, James B. (14. 9. 2007) [2004]. "Trigonometry". Arhivirano s originala, 2. 10. 2007. Pristupljeno 8. 11. 2015.
- ^ Edler von Braunmühl, Anton (1903). Vorlesungen über Geschichte der Trigonometrie - Von der Erfindung der Logarithmen bis auf die Gegenwart [Lectures on history of trigonometry - from the invention of logarithms up to the present] (jezik: German). 2. Leipzig, Germany: B. G. Teubner. str. 231. Pristupljeno 9. 12. 2015.CS1 održavanje: nepoznati jezik (link)
- ^ a b c d e f Cajori, Florian (1952) [1929]. A History of Mathematical Notations. 2 (2 (3rd corrected printing of 1929 issue) izd.). Chicago, USA: Open court publishing company. str. 172. ISBN 978-1-60206-714-1. 1602067147. Pristupljeno 11. 11. 2015.
The haversine first appears in the tables of logarithmic versines of José de Mendoza y Rios (Madrid, 1801, also 1805, 1809), and later in a treatise on navigation of James Inman (1821). See J. D. White in Nautical Magazine (February and July 1926).
(NB. ISBN and link for reprint of 2nd edition by Cosimo, Inc., New York, USA, 2013.) - ^ a b c d e f g h Shaneyfelt, Ted V. "德博士的 Notes About Circles, ज्य, & कोज्य: What in the world is a hacovercosine?". Hilo, Hawaii: University of Hawaii. Arhivirano s originala, 19. 9. 2015. Pristupljeno 8. 11. 2015.
- ^ a b c d e f g Cauchy, Augustin-Louis (1821). "Analyse Algébrique". Cours d'Analyse de l'Ecole royale polytechnique (jezik: French). 1. L'Imprimerie Royale, Debure frères, Libraires du Roi et de la Bibliothèque du Roi.CS1 održavanje: nepoznati jezik (link)[2] (reissued by Cambridge University Press, 2009; ISBN 978-1-108-00208-0)
- ^ a b c d e f g Bradley, Robert E.; Sandifer, Charles Edward (14. 1. 2010) [2009]. Buchwald, J. Z. (ured.). Cauchy’s Cours d’analyse: An Annotated Translation. Sources and Studies in the History of Mathematics and Physical Sciences. Cauchy, Augustin-Louis. Springer Science+Business Media, LLC. str. 10, 285. doi:10.1007/978-1-4419-0549-9. ISBN 978-1-4419-0548-2. LCCN 2009932254. 1441905499, 978-1-4419-0549-9. Pristupljeno 9. 11. 2015. (See errata.)
- ^ a b c d Weisstein, Eric W. "Vercosine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 24. 3. 2014. Pristupljeno 6. 11. 2015.
- ^ a b c d e f Weisstein, Eric W. "Coversine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 27. 11. 2005. Pristupljeno 6. 11. 2015.
- ^ a b c d e f Weisstein, Eric W. "Hacoversine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 29. 3. 2014. Pristupljeno 6. 11. 2015.
- ^ a b Ludlow, Henry Hunt; Bass, Edgar Wales (1891). Elements of Trigonometry with Logarithmic and Other Tables (3 izd.). Boston, USA: John Wiley & Sons. str. 33. Pristupljeno 8. 12. 2015.
- ^ a b Wentworth, George Albert (1903) [1887]. Plane Trigonometry (2 izd.). Boston, USA: Ginn and Company. str. 5.
- ^ a b Kenyon, Alfred Monroe; Ingold, Louis (1913). Trigonometry. New York, USA: The Macmillan Company. str. 8–9. Pristupljeno 8. 12. 2015.
- ^ a b Anderegg, Frederick; Roe, Edward Drake (1896). Trigonometry: For Schools and Colleges. Boston, USA: Ginn and Company. str. 10. Pristupljeno 8. 12. 2015.
- ^ a b c d Weisstein, Eric W. "Covercosine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 28. 3. 2014. Pristupljeno 6. 11. 2015.
- ^ a b c d e f g h Weisstein, Eric W. "Haversine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 10. 3. 2005. Pristupljeno 6. 11. 2015.
- ^ Fulst, Otto (1972). "17, 18". u Lütjen, Johannes; Stein, Walter; Zwiebler, Gerhard (ured.). Nautische Tafeln (jezik: German) (24 izd.). Bremen, Germany: Arthur Geist Verlag.CS1 održavanje: nepoznati jezik (link)
- ^ a b Sauer, Frank (2015) [2004]. "Semiversus-Verfahren: Logarithmische Berechnung der Höhe" (jezik: German). Hotheim am Taunus, Germany: Astrosail. Arhivirano s originala, 17. 9. 2013. Pristupljeno 12. 11. 2015.CS1 održavanje: nepoznati jezik (link)
- ^ Rider, Paul Reece; Davis, Alfred (1923). Plane Trigonometry. New York, USA: D. Van Nostrand Company. str. 42. Pristupljeno 8. 12. 2015.
- ^ "Haversine". Wolfram Language & System: Documentation Center. 7.0. 2008. Arhivirano s originala, 1. 9. 2014. Pristupljeno 6. 11. 2015.
- ^ a b Rudzinski, Greg (July 2015). Ix, Hanno. "Ultra compact sight reduction". Ocean Navigator. Portland, ME, USA: Navigator Publishing LLC (227): 42–43. ISSN 0886-0149. Pristupljeno 7. 11. 2015.
- ^ a b c d Weisstein, Eric W. "Havercosine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 29. 3. 2014. Pristupljeno 6. 11. 2015.
- ^ a b c d e f g van Vlijmen, Oscar (28. 12. 2005) [2003]. "Goniology". Eenheden, constanten en conversies (jezik: English). Arhivirano s originala, 28. 10. 2009. Pristupljeno 28. 11. 2015.CS1 održavanje: nepoznati jezik (link)
- ^ a b c d e Weisstein, Eric W. "Hacovercosine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 29. 3. 2014. Pristupljeno 6. 11. 2015.
- ^ a b Boyer, Carl Benjamin; Merzbach, Uta C. (6. 3. 1991) [1968]. A History of Mathematics (2 izd.). New York, USA: John Wiley & Sons. ISBN 978-0471543978. 0471543977.
- ^ a b "sagitta". Oxford English Dictionary (Online izd.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ a b Miller, Jeff (10. 9. 2007). "Earliest Known Uses of Some of the Words of Mathematics (V)". New Port Richey, Florida, USA. Arhivirano s originala, 5. 9. 2015. Pristupljeno 10. 11. 2015.
- ^ a b Šablon:OED2
- ^ White, J. D. (februar 1926). "(unknown title)". Nautical Magazine. (NB. According to Cajori, 1929, this journal has a discussion on the origin of haversines.)
- ^ White, J. D. (juli 1926). "(unknown title)". Nautical Magazine. (NB. According to Cajori, 1929, this journal has a discussion on the origin of haversines.)
- ^ a b Archibald, Raymond Clare (11. 7. 1945). "197: Natural and Logarithmic Haversines". Recent Mathematical Tables (PDF). Mathematical Tables and other Aids to Computation (MTAC) (Review). 1. The National Research Council, Division of Physical Sciences, Committee on Mathematical Tables and Other Aids to Computation; American Mathematical Society. str. 421–422. doi:10.1090/S0025-5718-45-99080-6. Arhivirano (PDF) s originala, 19. 11. 2015. Pristupljeno 19. 11. 2015. [3]
- ^ Farley, Richard (1856). Natural Versed Sines from 0 to 125°, and Logarithmic Versed Sines from 0 to 135°. London. (A haversine table from 0° to 125°/135°.)
- ^ Hannyngton, John Caulfield (1876). Haversines, Natural and Logarithmic, used in Computing Lunar Distances for the Nautical Almanac. London. (A 7-place haversine table from 0° to 180°, log. haversines at intervals of 15", nat. haversines at intervals of 10".)
- ^ Stark, Bruce D. (1997) [1995]. Stark Tables for Clearing the Lunar Distance and Finding Universal Time by Sextant Observation Including a Convenient Way to Sharpen Celestial Navigation Skills While On Land (2 izd.). Starpath Publications. ISBN 978-0914025214. 091402521X. Pristupljeno 2. 12. 2015.
- ^ Kalivoda, Jan (30. 7. 2003). "Bruce Stark - Tables for Clearing the Lunar Distance and Finding G.M.T. by Sextant Observation (1995, 1997)" (Review). Prague, Czech Republic. Arhivirano s originala, 12. 1. 2004. Pristupljeno 2. 12. 2015.[4][5]
- ^ Wildberger, Norman John (2005). Divine Proportions: Rational Trigonometry to Universal Geometry (1 izd.). Australia: Wild Egg Pty Ltd. ISBN 0-9757492-0-X. Pristupljeno 1. 12. 2015.
- ^ Stávek, Jiří (18. 10. 2013). "On the Trigonometric Loophole". Applied Physics Research. Prague, CZ: Canadian Center of Science and Education. 5 (6). doi:10.5539/apr.v5n6p48. eISSN 1916-9647. ISSN 1916-9639. Arhivirano s originala, 19. 11. 2015. Pristupljeno 19. 11. 2015.
- ^ a b c Simpson, David G. (8. 11. 2001). "AUXTRIG" (Fortran 90 source code). Greenbelt, Maryland, USA: NASA Goddard Space Flight Center. Arhivirano s originala, 16. 6. 2008. Pristupljeno 26. 10. 2015.
- ^ a b c van den Doel, Kees (25. 1. 2010). "jass.utils Class Fmath". JASS - Java Audio Synthesis System. 1.25. Arhivirano s originala, 2. 9. 2007. Pristupljeno 26. 10. 2015.
- ^ mf344 (4. 7. 2014). "Lost but lovely: The haversine". Plus magazine. maths.org. Arhivirano s originala, 18. 7. 2014. Pristupljeno 5. 11. 2015.
- ^ Skvarc, Jure (1. 3. 1999). "identify.py: An asteroid_server client which identifies measurements in MPC format". Fitsblink (Python source code). Arhivirano s originala, 20. 11. 2008. Pristupljeno 28. 11. 2015.
- ^ Skvarc, Jure (27. 10. 2014). "astrotrig.py: Astronomical trigonometry related functions" (Python source code). Ljubljana, Slovenia: Telescope Vega, University of Ljubljana. Arhivirano s originala, 28. 11. 2015. Pristupljeno 28. 11. 2015.
- ^ Weisstein, Eric W. "Inverse Haversine". MathWorld. Wolfram Research, Inc. Arhivirano s originala, 8. 6. 2008. Pristupljeno 5. 10. 2015.
- ^ "InverseHaversine". Wolfram Language & System: Documentation Center. 7.0. 2008. Pristupljeno 5. 11. 2015.
- ^ Woodward, Ernest (decembar 1978). Geometry - Plane, Solid & Analytic Problem Solver. Problem Solvers Solution Guides. Research & Education Association (REA). str. 359. ISBN 978-0-87891-510-1.
- ^ Needham, Noel Joseph Terence Montgomery (1959). Science and Civilisation in China: Mathematics and the Sciences of the Heavens and the Earth. 3. Cambridge University Press. str. 39. ISBN 9780521058018.
- ^ Boardman, Harry (1930). Table For Use in Computing Arcs, Chords and Versines. Chicago Bridge and Iron Company. str. 32.
- ^ Nair, P. N. Bhaskaran (1972). "Track measurement systems—concepts and techniques". Rail International. International Railway Congress Association, International Union of Railways. 3 (3): 159–166. ISSN 0020-8442. OCLC 751627806.





































