Talesova teorema

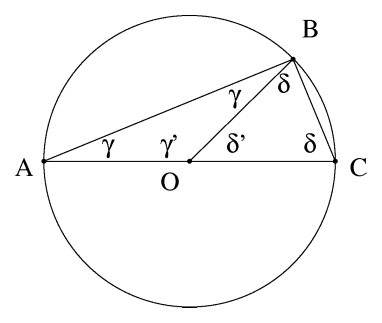
U geometriji, Talesova teorema (prema Talesu iz Mileta) kaže da ako su A,B i C tačke na kružnici, a gdje A i C čine promijer (dijametar) kruga, onda je ugao ABC pravi (pod 90 stepeni).

Dokaz

Koristimo sljedeće dokaze: suma uglova u trouglu je jednaka dva prava ugla (180 stepeni) i da su uglovi baza jednakokrakog trougla isti.

Neka O bude centar trougla. Pošto je OA=OB=OC, OAB i OBC su jednakokraki trouglovi, i po jednakosti uglova jednakokrakih trouglova imamo da je OBC=OCB i BAO=ABO. Neka $\gamma=BAO$ i $\delta=OBC$.

Pošto je suma uglova pravouglog trougla jednaka 180 stepeni, imamo:

2γ + γ ′ = 180°

i

2δ + δ ′ = 180°

...također, znamo da je

γ ′ + δ ′ = 180°

Sabirajući prve dvije jednačine i oduzimajući treću dobijamo

2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°

...što nakon poništavanja γ ′i δ ′, dobijamo:

γ + δ = 90°