Nedeterministički konačni automat
Ovaj članak ili neki od njegovih odlomaka nije dovoljno potkrijepljen izvorima (literatura, veb-sajtovi ili drugi izvori). |
U teoriji računanja, nedeterministički konačni automat (NKA) je konačni automat u kojem za svaki par stanja i ulaznog znaka (simbola) može postojati nekoliko mogućih sljedećih stanja.
Intuitivna objašnjenja[uredi | uredi izvor]
NKA obrađuje niz ulaznih znakova. Za svaki ulazni znak obavlja prijelaz u novo stanje sve dok svi ulazni znakovi nisu obrađeni.
Zovemo ga nedeterminističkim zato što se može dovesti u situaciju da postoje višestruki prijelazi iz trenutnog stanja koristeći isti znak. Za ε-NKA je također moguć prijelaz u novo stanje bez čitanja ulaznog znaka uopće. Na primjer, ako je neki fiktivni ε-NKA trenutno u stanju 1, a sljedeći ulazni znak jest a, on može preći u stanje 2 bez da obradi ijedan ulazni znak, kao i ući u stanje 3 čitanjem znaka a. NKA ne može odrediti koji je korektan prijelaz koji treba obaviti, te stoga ulazi u oba stanja.
Promjene stanja ε-NKA, a da se pri tome ne pročita ulazni znak, zovemo epsilon-prijelazi ili lambda-prijelazi. Obično se označavaju grčkim slovima ε ili λ.
Kada NKA pročita sve znakove ulaznog niza, on prihvaća niz ako i samo ako postoji neki slijed prijelaza koje može načiniti a koji će ga dovesti u prihvatljivo stanje. Shodno tome, ne prihvaća (odbija) niz znakova ako bez obzira koje izbore učini prilikom prijelaza u neki element skupa od više stanja, neće završiti u nekom od prihvatljivih stanja.
Formalna definicija[uredi | uredi izvor]
Nedeterministički konačni automat (NKA) se formalno definira kao uređena petorka, (S, Σ, T, s0, A), koju čini:
- konačni skupa stanja (S)
- konačni skup ulaznih znakova (Σ)
- funkcija prijelaza (T : S × (Σ ∪{ε}) → P(S)).
- istaknuti skup stanja s0 kojeg zovemo početni (ili inicijalni) skup stanja (s0 ⊆ S)
- istaknuti skup stanja A kojeg zovemo skup prihvatljivih (ili finalnih) stanja (A ⊆ S)
gdje je P(S) partitivni skup (skup svih podskupova) skupa S, ε prazni niz, a Σ ulazna abeceda
Neka je M NKA takav da M = (S, Σ, T, s0, A), i X je niz znakova nad abecedom Σ. M prihvaća niz X ako postoji i reprezentacija niza X oblika x1x2 ... xn, xi ∈ (Σ ∪{ε}), i slijed prijelaza stanja r0,r1, ..., rn, ri ∈ S koji zadovoljava sljedeće uvjete:
- r0 ∈ s0
- ri ∈ T(ri-1, xi ), for i = 1, ..., n
- rn ∈ A.
Stroj započinje rad u proizvoljnom početnom stanju te potom čita niz znakova svoje ulazne abecede. Automat koristi relaciju prijelaza T da odredi sljedeće stanje koristeći trenutno stanje te znak upravo pročitan ili prazni niz (u slučaju ε-prijelaza). Međutim, sljedeće stanje NKA ne ovisi samo o trenutnom ulaznom događaju (tj. trenutno pročitanom znaku), već i o proizvoljnom broju narednih ulaznih događaja. Sve dok se ti sljedeći ulazni događaji ne dogode (tj. znakovi se ne pročitaju), nije moguće odrediti stanje u kojem se stroj nalazi. Ako se po završetku čitanja ulaznog niza automat nalazi u prihvatljivom stanju, kažemo da NKA prihvata niz, inače kažemo da ga ne prihvata (odbija).
Skup svih nizova znakova koje NKA prihvata zovemo jezikom koji NKA prihvata. Taj jezik je regularni jezik.
Za svaki NKA može biti konstruisan istovjetni DKA, tj. DKA koji prihvata isti jezik. Stoga je moguće obaviti konverziju već postojećeg NKA u DKA u svrhu implementiranja jednostavnijeg stroja. Takva konverzija može dovesti do eksponencijalnog rasta u broju potrebnih stanja stroja.
Ostvarenje[uredi | uredi izvor]
Postoji mnogo načina za ostvarenje NKA:
- Konvertiraj u istovjetni DKA. U nekim će slučajevima doći do eksponencijanog rasta u veličini automata (posebno broju potrebnih stanja) a time i pomoćnog prostora proporcionalnog broju stanja NKAa (s obzirom da spremanje vrijednosti stanja zahtijeva najviše jedan bit za svako stanje NKAa).
- Održavaj podatkovnu strukturu skup (konačni asocijativni kontejner bez ponavljanja vrijednosti) koja će sadržavati sva stanja u kojima stroj trenutno može biti. Prilikom čitanja posljednjeg ulaznog znaka, ukoliko je jedno od stanja konačno stanje, stroj prihvata niz znakova. U najgorem slučaju, ovo može zahtijevati pomoćni prostor veličine proporcionalne broju stanja NKA; ako podatkovna struktura skup koristi tačno jedan bit po stanju NKAa, ovo ostvarenje je istovjetno prethodnom.
- Stvaramo višestruke kopije. Za svaku odluku o grananju u n stanja, NKA kreira do kopija stroja. Svaka kopija ulazi u odvojeno stanje. Ako se, prilikom čitanja posljednjeg ulaznog znaka, barem jedna kopija NKAa nalazi u prihvatljivom stanju, NKA prihvata ulazni niz znakova. (Ovo ostvarenje također zahtijeva linearni prostor za spremanje s obzirom na broj stanja NKAa, budući da može biti postojati po jedan stroj za svako stanje NKAa).
- Eksplicitno propagiraj pojedine znakove kroz prijelaznu strukturu NKAa i zabilježi kad god znak dostigne prihvatljivo stanje. Ovo je ponekad korisno kad NKA treba zakodirati dodatni kontekst o događajima koji su potaknuli prijelaz. (Za programsko ostvarenje ove tehnike koja prati reference na objekt pogledati papir koji je implementira pod nazivom Tracematches Arhivirano 8. 3. 2008. na Wayback Machine.)
Primjer[uredi | uredi izvor]
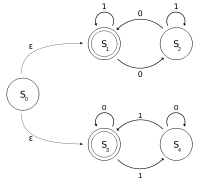
Sljedeći primjer objašnjava NKA M koji operiše nad binarnom abecedom i koji odlučuje sadrži li ulazni niz znakova paran broj brojki 0 ili paran broj brojki 1.
M = (S, Σ, T, s0, A) gdje je
- Σ = {0, 1},
- S = {S0, S1, S2, S3, S4},
- s0 = {S0},
- A = {S1, S3}, and
- Funkcija prijelaza T može biti definirana sljedećom tablicom prijelaza:
Dijagram stanja za M jest:
M se može shvatiti kao unija dva DKAa: jednog sa skupom stanja {S2, S1} i drugog sa skupom stanja {S3, S4}.
Jezik automata M može biti opisan sljedećim regularnim izrazom:
Također pogledajte[uredi | uredi izvor]
Reference[uredi | uredi izvor]
- Michael Sipser. Introduction to the Theory of Computation. PWS, Boston. 1997. ISBN 0-534-94728-X. Section 1.2: Nondeterminism, pp. 47–63.
- Siniša Srbljić. Jezični Procesori. Element, Zagreb. 2003. ISBN 953-197-129-3. Sekcija 2.1.3: Nedeterministički konačni automat (NKA), pp. 29–34.
| Commons ima datoteke na temu: Nedeterministički konačni automat |