Hagen–Poiseuilleova jednačina
| Mehanika kontinuuma | |
|---|---|
| | |
Hagen–Poiseuilleova jednačina je fizikalni zakon koji opisuje sporo viskozno nestišljivo strujanje kroz konstantni kružni poprečni presjek. Poznat je i kao Hagen–Poiseuilleov zakon, Poiseuilleov zakon i Poiseuilleov jednačina. Nazvana je po njemačkom inženjeru i fizičaru Gotthilfu Hagenu i francuskom fizičaru i fiziologu Jean-Léonard-Marieju Poiseuilleu.
Jednačina[uredi | uredi izvor]
Standardno označavanje u dinamici fluida[uredi | uredi izvor]
U standrardnom označavanju u dinamici fluida:
ili
gdje je
- pad pritiska
- L dužina cijevi
- dinamička viskoznost
- Q is the zapreminski protok
- r is the radijus
- d is the dijametar
- matematička konstanta pi (približno 3,141592654).
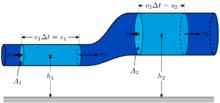
Fizikalno označavanje[uredi | uredi izvor]
gdje je:
- V zapremina tečnosti koja protiče (kumbi metar)
- t vrijeme (sekunda)
- v srednja brzina fluida uzduž cijevi (metar/sekunda)
- x udaljenost u pravcu strujanja (metar)
- R unutrašnji radijus cijevi (metar)
- ΔP razlika u pritisku između dva kraja (paskal)
- η je dinamička viskoznost fluida (paskal-sekunda (Pa·s)),
- L ukupna dužina cijevi u x pravcu (metar).
Veza sa Darcy–Weisbachom[uredi | uredi izvor]
Ovaj rezultat je, također, rješene fenomenološke Darcy–Weisbachove jednačine u oblasti hidraulike, dajući odnos koeficijenta trenja preko Reynoldsovog broja:
gdje je Re Reynoldsov broj, a ρ je gustoća fluida. U ovom obliku, zakon aproksimira Darcyjev koeficijent trenja, koeficijent gubitka energije, koeficijent gubitka trenja ili Darcyjev koeficijent Λ u laminarnom strujanju pri niskim brzinama u cilindričnoj cijevi. Teoretsku derivaciju blago izmijenjenog oblika ovog zakon nezavisno su napravili Wiedman 1856. i Neumann i E. Hagenbach 1858. godine (1859. i 1860. godine). Hagenbach je bio prvi koji je nazvao ovaj zakon Poiseuilleovim zakonom.
Ovaj zakon posebno je važan u hemodinamici, jednoj od podoblasti fiziologije.[1]
Poiseuilleov zakon je kasnije, 1891. godine, proširen i na turbulentno strujanje od strane L. R. Wilberforcea, čiji je rad osnovan na Hagenbachovom radu.
Derivacija[uredi | uredi izvor]
Hagen–Poiseuilleova jednačina može se dobiti iz Navier–Stokesovih jednačina.
Analogija sa električnim krugovima[uredi | uredi izvor]
Elektricitet je najprije shvaćen kao neka vrsta fluida. Ova hidraulička analogija je još uvijek konceptualno korisna.
Poiseuilleov zakon odgovara Ohmovom zakonu za električne krugove (U = IR), gdje je pad pritiska ΔP analogan sa naponom U, a zapreminski protok Φ je analogan struji I. Tada je otpor
Ovaj koncept je koristan jer je efektivni otpor u cijevi obrnuto proporcionalan četvrtom stepenu radijusa. Ovo znači da ako prepolovimo veličinu cijevi, otpor kretanju fluida povećat će se 16 puta.
I Ohmov i Poiseuilleov zakon ilustruju transportni fenomen.
Reference[uredi | uredi izvor]
- S. P. Sutera, R. Skalak, "The history of Poiseuille's law," Annual Review of Fluid Mechanics, Vol. 25, 1993, pp. 1–19
- Pfitzner, J (1976), "Poiseuille and his law.", Anaesthesia (objavljeno mart 1976), 31 (2), str. 273–5, PMID:779509
Također pogledajte[uredi | uredi izvor]
Vanjski linkovi[uredi | uredi izvor]
| Commons ima datoteke na temu: Hagen–Poiseuilleova jednačina |









