Leonhard Euler
| Leonhard Euler | |
|---|---|
 | |
| Rođenje | 15. april 1707. Basel, Švicarska |
| Smrt | 18. septembar 1783 (76 godina) Sankt Peterburg, Rusko Carstvo |
| Prebivalište | |
| Državljanstvo | Švicarsko |
| Narodnost | Švicarac |
| Polje | Matematika i fizika |
| Alma mater | Univerzitet u Baselu |
| Akademski mentor | Johann Bernoulli |
| Istaknuti studenti | Johann Friedrich Hennert |
| Mehanika kontinuuma | |
|---|---|
|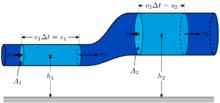 | |
Leonhard Euler (rođen 15. aprila 1707) bio je švicarski matematičar, fizičar, astronom i inženjer koji je otkrio i definirao važne stvari u mnogim granama matematike, kao što su Infinitezimalni račun i teorija grafova, a ostvario je i pionirski doprinos na nekoliko različitih naučnih polja, kao što su topologija i analitička teorija brojeva. Također je uveo većinu savremene matematičke terminologije i notacije, posebno na polju matematičke analize, kao što je pojam matematičke funkcije.[1] Poznat je i po radu i doprinosu na polju mehanike, dinamike fluida, optike, astronomije i teorije muzike.[2]
Bio je jedan od najeminentnijih matematičara 18. vijeka i smatra se jednim od najvećih u historiji. Također se smatra da je bio najplodniji matematičar svih vremena. Njegovi sabrani radovi sačinjavaju 60 do 80 Quartova, više od bilo koga drugog matematičara. Veći dio punoljetstva proveo je u ruskom Sankt Peterburgu i Berlinu, tadašnjem glavnom gradu Pruske.
Izjava pripisana također poznatom matematičaru Pierre-Simon Laplasu izražava Eulerov utjecaj na matematiku: Čitajte Eulera, čitajte Eulera, on je najveći od svih nas.[3]
Biografija[uredi | uredi izvor]
Rani period[uredi | uredi izvor]
Rođen je 15. aprila 1707. u švicarskom Baselu od oca Paula i majke Margarite. Imao je dvije mlađe sestre Ana Mariju i Mariju Magdalenu i mlađeg brata Johana Heinricha. Ubrzo po rođenju sa porodicom se preselio u grad Riehen, gdje je proveo većinu svog djetinjstva. Paul Euler, Leonhardov otac bio je prijatelj porodice Bernoulli. Johann Bernoulli je tada smatran za najboljeg matematičara u Evropi i na kraju je u najvećoj mjeri i uticao na mladog Leonharda.
Formalno obrazovanje započeo je u Baselu, gdje je poslat da živi s bakom. Sa 13 godina (1720) upisuje se na Univerzitet u Baselu, a 1723. godine stiče diplomu magistra filozofije sa disertacijom koja upoređuje filozofije Descartesa i Newtona. Tokom tog perioda, uzimao je subotnje popodnevne časove kod Johanna Bernoulija, koji je ubrzo otkrio nevjerovatni talenat za matematiku kod svog novog učenika. U to vrijeme Eulerova glavna preokupacija se sastojala iz proučavanja teologije i učenja grčkog i hebrejskog jezika pod uticajem oca koji je želio da Leonhard postane pastor kao i on sam. Međutim, Bernoulli je ipak ubjedio njegovog oca da je Leonhardu predodređeno da postane veliki matematičar.
Godine 1726. završava disertaciju o širenju zvuka pod naslovom De Sono. U to vrijeme, bezuspješno je pokušavao da stekne poziciju na Univerzitetu u Baselu. Godine 1727. se prvi put prijavljuje na konkurs Francuske akademije nauka, a vezano za iznalaženje najboljeg načina postavljanja jarbola na brod. Međutim, prvu nagradu osvaja Pierre Bouguer, koji je postao poznat kao otac pomorske arhitekture dok Euler osvaja drugo mjesto. Tokom kasnijeg perioda Euler će ovu godišnju nagradu osvajati 12 puta.
Sankt Peterburg[uredi | uredi izvor]

Otprilike u to vrijeme, dva sina Johanna Bernulija, Danijel i Nikolas su radili na Ruskoj akademiji nauka u Sankt Peterburgu. Dana 31. jula 1726. godine, nakon manje od godine provedene u Rusiji,[4][5] Nikolas umire od upale crvuljka, na njegovo mjesto u odjelu za matematiku i fiziku prelazi Danijel a predlaže Eulera na mjesto u odjeljenju za fiziologiju. Predloženo mjesto Euler nestrpljivo prihvata u novembru 1726. ali odlaže odlazak u Sankt Peterburg zbog prijave za profesora fizike na Univerzitetu u Baselu, koja na kraju završava bezuspješno.
Pa ipak 17. maja 1727. godine odlazi u Sankt Peterburg. Biva promovisan sa nižeg položaja u medicinskom odeljenju na položaj u matematičkom odeljenju. U tom periodu stanuje zajedno sa Danijelom sa kojim često blisko sarađuje. Savladava ruski jezik i organizuje svoj život u Sankt Peterburgu. Također pronalazi dodatni posao ljekara u ruskoj mornarici.
Akademija u Sankt Peterburgu, koju je osnovao Petar Veliki, imala je za cilj poboljšanje stepena obrazovanja u Rusiji i smanjenje razlike na polju naučnog rada između tadašnjeg carstva i država zapadne Evrope. Kao rezultat toga, Akademija se činila posebno atraktivno za strane stipendiste poput Eulera. Akademija nije oskudjevala finansijskim sredstvima a uz to posjedovala je sveobuhvatnu biblioteku, uglavnom formiranu od privatnih biblioteka Petra i plemstva. Na Akademiju je upisivan vrlo mali broj studenata kako bi se smanjilo opterećenje za nastavnike a samim time dalo im se više vremena za istraživanje i bavljenje naučnim radom. Takvu politiku nastavila je i Katarina I koja umire 1727. godine a dolaskom na vlast dvanaestogodišnjeg vladara Petra II pojačava se sumnjičavost prema inostranom akademskom osoblju čime se smanjuje finansiranje Akademije što prouzrokuje finansijske probleme za Eulera i njegove kolege.
Uslovi se neznatno popravljaju nakon smrti Petra II a Euler ubrzano hijerarhijski napreduje te postaje profesor fizike 1731. godine. Dvije godine kasnije, odlaskom Danijela Bernoullija u Basel, Euler preuzima mjesto šefa matematičkog odjela.
Dana 7. januara 1734. ženi Katharinu Gsell (1707–1773), kćerku švicarskog baroknog slikara Georga Gsela. Mladi bračni par kupuje kuću pored rijeke Neve a od 13 rođene djece njih samo petoro preživljava djetinjstvo.[6]
Berlin[uredi | uredi izvor]
Zabrinut zbog kontinuiranih političkih previranja u Rusiji, zajedno sa porodicom Euler 19. juna 1741. godine napušta Sankt Peterburg da bi preuzeo dužnost na berlinskoj akademiji, koju mu je ponudio kralj Pruske Fridrik II. U Berlinu je proveo 25 godina i u tom periodu je napisao više od 380 članaka. Također, objavio je i dva djela koja su ga najviše proslavila: Uvod u infinitezimalnu analizu, tekst o funkcijama objavljen 1748. i djelo Osnove integralnog računa objavljeno 1755. a koje je tretiralo problem diferencijalnog računa. Godine 1755. izabran je za stranog člana Švedske kraljevske akademije nauka.
Osim toga, od Eulera je zatraženo da podučava Friederiku Charlotte iz Brandenburg-Schwedta, princezu Vojvodstva Anhalt-Dessau i nećaku Fridrika II. Tokom perioda s početka 1760-ih Euler je napisao i oko 200 pisama princezi Friederiki koja su kasnije obrađena i postala bestseller pod nazivom Pisma njemačkoj princezi o raznim stvarima iz oblasti fizike i filozofije. Tu se nalaze i Eulerove analize o raznim temama vezanim za fiziku i matematiku a pružaju i dragocjen uvid u Eulerovu ličnost i vjerska uvjerenja. Knjiga je postala čitljivija od svih njegovih matematičkih radova a objavljena je širom Evrope i Sjedinjenih Američkih Država. Popularnost pisama svjedoči o sposobnosti Eulera da o naučnim pitanjima i problemima efikasno komunicira sa publikom, što je rijetka sposobnost za naučnika ili istraživača.
Pogoršanje vida[uredi | uredi izvor]

Stanje s Eulerovim vidom se pogoršavalo tokom njegove matematičke karijere. Godine 1738. postao je gotovo slijep na desno oko, za što je prema Euleru bio uglavnom zaslužan mukotrpan rad na kriptografiji tokom boravka u Sankt Peterburgu. Eulerov vid na desno oko se tokom boravka u Njemačkoj toliko pogoršao da ga je Fridrik nazvao Kiklopom. Poslije toga, 1766. godine otkrivena mu je i siva mrena na lijevom oku. Samo nekoliko nedjelja nakon tog otkrića Euler je postao skoro slijep. Međutim, to stanje skoro da nije imalo uticaja na njegovu produktivnost, tu vrstu ograničenja nadoknađivao je svojim mentalnim vještinama i izuzetnom memorijom. Kada je izgubio vid na oba oka, Euler je izjavio: "Sada ću imati manje smetnji i odvraćanja pažnje".
Primjera radi, Euler je bio u stanju recitovati Vergilijevu Eneidu od početka do kraja, a za svaku stranicu mogao je navesti koji redak je na vrhu a koji na dnu stranice. Uz pomoć svojih pisara, Eulerova produktivnost je u mnogim područjima čak i povećana. Tokom 1775. u prosjeku je pisao po jedan matematički rad svake nedjelje.
Povratak u Rusiju i smrt[uredi | uredi izvor]
Godine 1760, tokom Sedmogodišnjeg rata, ruske trupe u napredovanju pljačkaju Eulerovu farma u Charlottenburgu. Nakon ovog događaja, general Ivan Petrovič Saltykov je platio nadoknadu štete prouzrokovanu Eulerovom imanju a kasnije je i carica Rusije Elizabeta dodala tom iznosu svotu od 4.000 rubalja, u to doba pretjerano visok iznos.[7] Politička situacija u Rusiji stabilizovana je nakon dolaska Katarine II na prijestol, tako da je Euler 1766. godine prihvatio poziv da se vrati na akademiju u Sankt Peterburgu.
Njegovi uslovi bili su prilično iznenađujući. Zahtjevao je godišnju platu od 3000 rublji, penziju za suprugu i obećanje visokog imenovanja za svoje sinove. Svi njegovi zahtjevi su odobreni. Ostatak svog života proveo je u Rusiji. Međutim, njegov drugi boravak u Rusiji obilježen je tragedijama. Prvo mu je 1771. godine izgorio dom u Sankt Peterburgu pri čemu je skoro izgubio život. Dvije godine poslije, 1773. preminula mu je supruga Katarina, nakon 40 godina braka. Tri godine nakon smrti supruge, Euler se oženio njenom polusestrom, Salome Abigail Gsell (1723–1794).[8] U tom braku će ostati do njegove smrti. 1782. izabran je za inostranog počasnog člana Američke akademije umjetnosti i nauka[9].
Dana 18. septembra 1783. u Sankt Peterburgu, nakon ručka sa svojom porodicom, Euler je razgovarao o novootkrivenoj planeti Uran i njenoj orbiti sa kolegom akademikom Andersom Johanom Lexellom, kada se srušio od krvarenja mozga. Umro je nekoliko sati kasnije.
Jacob von Staehlin-Storcksburg napisao je kratak nekrolog za Rusku akademiju nauka dok je ruski matematičar Nicolas Fuss, jedan od Eulerovih učenika, napisao detaljniju eulogiju koju je pročitao na komemoraciji.
U eulogiji za Francusku akademiju, francuski matematičar i filozof Marquis de Condorcet, napisao je:
il cessa de calculer et de vivre -... prestao je da računa i živi.
Sahranjen je pored prve supruge Katarine na smolenskom luteranskom groblju, na ostrvu Goloday. 1785. godine, Ruska akademija nauka postavila je mermerno poprsje Leonharda Eulera na postolje pored sjedišta Direktora a 1837. postavljen je i kamani nadgrobni spomenik. Tokom obilježavanja 250. godišnjice rođenja Eulera, nadgrobni spomenik zajedno sa posmrtnim ostacima premješten je na groblje Aleksandra Nevskog.
Doprinos matematici i fizici[uredi | uredi izvor]
Euler je proučavao skoro sve oblasti matematike, između ostalih geometriju, infinitezimalni račun, trigonometriju, algebru i teoriju brojeva, a tema njegovog naučnog ineresovanja bile su i oblasti fizike poput mehanika kontinuuma, lunarna teorija i druge oblasti fizike. Za Eulera se može reći da je zapažena figura u historiji matematike. Njegovi radovi, da se odštampaju, od kojih su mnogi od fundamentalnog značaja, zauzeli bi između 60 i 80 quartova. Eulerovo ime povezano je sa velikim brojem tema.
Euler je jedini matematičar u čast kojeg su nazvana dva broja u matematici. Važniji i poznatiji broj koji je nazvan po Euleru je broj e, čija je vrijednost približno jednaka 2,71828, a drugi broj je ustvari Euler-Mascheronijeva konstanta (γ) a koja se ponekad jednostavno naziva i Eulerova konstanta a čija približna vrijednost iznosi 0,57721.
Matematička notacija[uredi | uredi izvor]
Euler je u oblast matematičke notacije uveo nekoliko konvencija koje je popularizovao kroz svoje brojne i široko rasprostranjene radove i udžbenike. Kao najvažnije za spomenuti, prvi je predstavio koncept funkcije f(x) gdje je sa f označio funkciju koja se primjenjuje na x. Osim toga, predstavio je i savremenu notaciju za trigonometrijske funkcije, slovo e kao oznaku za bau ili osnovu prirodnog logaritma (danas poznat i kao Eulerov broj), grčko slovo Σ koje se koristi kao oznaka za sumu kao i slovo i kojim se označava imaginarna jedinica. Također je koristio i popularizovao grčko slovo π da označi odnos između obima i prečnika kruga, iako taj odnos nije otkrio Euler već velški matematičar William Jones.
Analiza[uredi | uredi izvor]
Razvoj infinitezimalnog računa je bio u prvom planu matematičkih istraživanja tokom 18. vijeka, a članovi Bernulijeve porodice, koji su bili prijatelji Eulera, su zaslužni za veliki napredak na tom polju. Zahvaljujući njihovom uticaju, proučavanje ovog računa postaje glavni fokus Eulerovog rada. Dok njegovi pojedini dokazi nisu prihvatljivi savremenim matematičkim standardima (naročito njegovo oslanjanje na princip opšte algebre), neke njegove ideje dovele su do mnogih velikih otkrića. Euler je dobro poznat na polju matematičke analize zbog učestale upotrebe i razvoja potencijalnog reda, odnosno predstavljanja funkcija kao sume beskonačno mnogo članova koja se može predstaviti sljedećim izrazom:
Osim toga, značajno je napomenuti da je Euler direktno dokazao vrijednost potencijalnog reda kroz primjere broja e i inverzne trigonometrijske funkcije. (Indirektni dokaz pomoću tehnike inverznog potencijalnog reda, odnosno niza dali su također poznati matematičari Newton i Leibniz između 1670. i 1680. godine). Njegova sjmela upotreba potencijalnog reda omogućila mu je da riješi poznati Bazelski problem 1735. godine (detaljniji argument za rješenje problema priložio je 1741. godine):
Euleru se pripisuje uvođenje eksponencijalne funkcije i logaritama u analitičke dokaze. Otkrio je kako izraziti različite logaritamske funkcije koristeći potencijalne redove a također je uspješno definirao logaritme negativnih i kompleksnih brojeva čime je u velikoj mjeri proširio područje matematičke primjene logaritama. Osim toga definirao je i eksponencijalnu funkciju za kompleksne brojeve pri čemu je otkrio i njenu vezu sa trigonometrijskim funkcijama. Za bilo koji relni broj φ prema Euleru vrijedi izraz:
Specijalni slučaj izraza iznad, poznat kao Eulerov identitet
Richard Feynman u svom djelu smatra za najznačajniju formulu u matematici, jer se u jednom izrazu, uz upotrebu različitih matematičkih operacija (sabiranje, množenje i stepenovanje) predstavlja pet značajnih konstanti u matematici a to su: 0, 1, e, i i π. Čitaoci časopisa Mathematical Intelligence su 1988. godine glasali za Najljepšu matematičku formulu ikada. Značajno je napomenuti da se među pet prvoplasiranih našlo čak tri Eulerove formule.
De Moivreova formula je direktna posljedica Eulerove formule.
Osim navedenog, Euler je obrazložio teoriju viših transcendentnih funkcija uvođenjem gama funkcije kao i uvođenjem nove metode za rješavanje jednačina četvrtog stepena. Otkrio je i način računanja integrala sa kompleksnim granicama predodređujući time razvoj savremene kompleksne analize. Također je pronašao varijacijski račun, uključujući njegov najpoznatiji rezultat, Euler-Lagrangeovu jednačinu.
Euler је također bio pionir koji je koristio analitičke motede s ciljem rješavanja problema iz oblasti teorije brojeva. Upravo iz toga razloga, ujedinio je dvije različite grane matematike uvodeći pri tome novu oblast istraživanja, analitičku teoriju brojeva. U toku uvođenja nove oblasti u matematici, formirao je teoriju hipergeometrijskih redova, q-redova, hiperboličnih trigonometrijskih funkcija i analitičku teoriju verižnih ralomaka. Primjera radi, dokazao je da prostih brojeva ima beskonačno mnogo koristeći divergentnost harmonijskih redova a koristio je i analitičke metode kako bi odgonetnuo kako su prosti brojevi raspoređeni unutar skupa prirodnih brojeva. Eulerovi radovi na ovom polju doprinjeli su razvoju teorema o prostim brojevima.
Teorija brojeva[uredi | uredi izvor]
Eulerov interes za teoriju brojeva potakao je Christiana Goldbacha, njegov prijatelj sa akademije u Sankt Peterburgu. Veliki dio njegovih najranijih radova iz ove oblasti je bilo zasnovano na djelima Pierrea de Fermata. Euler je razvio neke njegove ideje ali je i opovrgao nekoliko hipoteza.
Povezao je prirodu pojavljivanja prostih brojeva sa idejama matematičke analize. Dokazao je da je suma recipročnih vrijednosti prostih brojeva divergira, otkrivši pri tome vezu između Rimanove zeta-funkcije i prostih brojeva, danas poznatu kao Eulerova formula za Rimanovu zeta-funkciju.
Dokazao je i Newtonove identitete, Malu Fermatovu teoremu, Fermatovu teoremu o zbiru dva kvadrata i značajno doprinjeo Lagrangeovoj teoremi o četiri kvadrata.
Također pogledajte[uredi | uredi izvor]
- d'Alembert–Eulerov uslov
- Eulerov broj, baza prirodnog logaritma, poznat i kao Napierova konstanta
Refernce[uredi | uredi izvor]
- ^ Dunham 1999, str. 17
- ^ Saint Petersburg (1739). "Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae". Pristupljeno 18. 6. 2018.
- ^ Dunham, William (1999). Euler: The Master of Us All. Mathematical Association of America. ISBN 978-0-88385-328-3.
- ^ Ronald Calinger. Leonhard Euler: The First St. Petersburg Years (1727–1741). Historia Mathematica 23, 2 (1996), 121-166, read online
- ^ O'Connor, John J.; Robertson, Edmund F. "Nicolaus(II) Bernoulli". MacTutor History of Mathematics archive. University of St Andrews. Pristupljeno 24. 1. 2016.
- ^ Fuss, Nicolas. "Eulogy of Leonhard Euler". Pristupljeno 19. 6. 2018.
- ^ Gindikin, S.G., Гиндикин С. Г., МЦНМО, НМУ, 2001, с. 217.
- ^ Gekker, I. R.; Euler, A. A. "Leonhard Euler's family and descendants". Bogolyubov, Mikhaĭlov i Yushkevich 2007, str. 402. Upotreblja se zastarjeli parametar
|chapterurl=(pomoć) - ^ ""Book of Members, 1780–2010: Chapter E" (PDF). American Academy of Arts and Sciences" (PDF). amacad.org. Pristupljeno 26. 6. 2018.
Literatura[uredi | uredi izvor]
- Lexikon der Naturwissenschaftler, (2000), Heidelberg: Spektrum Akademischer Verlag.
- Bradley, Robert E.; D'Antonio, Lawrence A.; Sandifer, Charles Edward (2007). Euler at 300: An Appreciation. Mathematical Association of America. ISBN 978-0-88385-565-2.
- Calinger. Ronald S. Leonhard Euler: Mathematical Genius in the Enlightenment (Princeton UP, 2016). Pp. xvii, 669.
- Demidov, S.S. (2005). "Treatise on the differential calculus". u Grattan-Guinness, Ivor (ured.). Landmark Writings in Western Mathematics 1640–1940. Elsevier. str. 191–98. ISBN 978-0-08-045744-4.
- Dunham, William (2007). The Genius of Euler: Reflections on his Life and Work. Mathematical Association of America. ISBN 978-0-88385-558-4.
- Fraser, Craig G. (11. 2. 2005). Leonhard Euler's 1744 book on the calculus of variations. ISBN 978-0-08-045744-4. In Grattan-Guinness 2005, str. 168–80
- Gautschi, Walter (2008). "Leonhard Euler: his life, the man, and his works" (PDF). SIAM Review. 50 (1): 3–33. Bibcode:2008SIAMR..50....3G. CiteSeerX 10.1.1.177.8766. doi:10.1137/070702710.
- Hascher, Xavier and Papadopoulos, Athanase (editors). 2015. Leonhard Euler : Mathématicien, physicien et théoricien de la musique, Paris, CNRS Editions, 2015, 516 str.
- Heimpell, Hermann, Theodor Heuss, Benno Reifenberg (editors). 1956. Die großen Deutschen, volume 2, Berlin: Ullstein Verlag.
- Krus, D.J. (novembar 2001). "Is the normal distribution due to Gauss? Euler, his family of gamma functions, and their place in the history of statistics". Quality & Quantity. 35 (4): 445–46. doi:10.1023/A:1012226622613. Arhivirano s originala, 10. 2. 2006.
- Nahin, Paul J. (2006). Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills. Princeton University Press. ISBN 978-0-691-11822-2.
- du Pasquier, Louis-Gustave (2008). Leonhard Euler And His Friends. Prevod: John S.D. Glaus. CreateSpace. ISBN 978-1-4348-3327-3.
- Reich, Karin (11. 2. 2005). 'Introduction' to analysis. ISBN 978-0-08-045744-4. In Grattan-Guinness 2005, str. 181–90
- Richeson, David S. (2011). Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. ISBN 978-0-691-12677-7.
- Sandifer, C. Edward (2007). The Early Mathematics of Leonhard Euler. Mathematical Association of America. ISBN 978-0-88385-559-1.
- Sandifer, C. Edward (2007). How Euler Did It. Mathematical Association of America. ISBN 978-0-88385-563-8.
- Simmons, J. (1996). The giant book of scientists: The 100 greatest minds of all time. Sydney: The Book Company. ISBN 978-1-86309-647-8.
- Singh, Simon (1997). Fermat's Last Theorem. New York: Fourth Estate. ISBN 978-1-85702-669-6.
- Thiele, Rüdiger (2005). "The mathematics and science of Leonhard Euler". u Kinyon, Michael; van Brummelen, Glen (ured.). Mathematics and the Historian's Craft: The Kenneth O. May Lectures. Springer. str. 81–140. ISBN 978-0-387-25284-1.
- "A Tribute to Leohnard Euler 1707–1783". Mathematics Magazine. 56 (5). novembar 1983.
- Derbyshire, John (2003). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. Washington, DC: John Henry Press. ISBN 978-0-309-08549-6..
Vanjski linkovi[uredi | uredi izvor]
| Commons ima datoteke na temu: Leonhard Euler |
- Mehanika kontinuuma
- Leonhard Euler
- Rođeni 1707.
- Umrli 1783.
- Biografije, Basel
- Švicarski matematičari
- Švicarski fizičari
- Matematički analitičari
- Balističari
- Dinamičari fluida
- Teoretičari brojeva
- Optički fizičari
- Članovi Francuske akademije nauka
- Članovi Pruske akademije nauka
- Članovi Kraljevskog društva
- Članovi Kraljevske švedske akademije nauka





