1 + 1 + 1 + 1 + · · ·

1 + 1 + 1 + 1 + · · ·

poslije izravnanja

1 + 1 + 1 + 1 + · · ·, može se pisati i kao $\sum _{n=1}^{\infty }n^{0}$, $\sum _{n=1}^{\infty }1^{n}$, ili $\sum _{n=1}^{\infty }1$, je divergentni red. To znači da niz parcijalnih suma ne konvergira do neke granice u skupu realnih brojeva.

Niz $1^{n}$ može se posmatrati kao geometrijski niz sa zajedničkim odnosom $1$. Za razliku od drugih geometrijskih nizova sa racionalnim odnosom (osim -1), ne konvergira u realne brojeve.

Kada se pojavi u primjeni u fizici, red 1 + 1 + 1 + 1 + · · · se može interpretirati pomoću regularizacije zeta funkcije. To je vrijednost Riemannove zeta funkcije za $s=0$

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}\,$ $={\frac {1}{1-2^{1-s}}}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}\,,$

Gore navedene formule ne važe za nulu, međutim, kako jedna mora da koristi analitički nastavak Rimanove zeta funkcije,

Asimptotsko ponašanje izravnanja. U-presjek linije je $-1/2$

$\zeta (s)=2^{s}\pi ^{s-1}\ \sin \left({\frac {\pi s}{2}}\right)\ \Gamma (1-s)\ \zeta (1-s)\!,$

Koristeći ovaj dobija se (s obzirom da je $\Gamma (1)=1$),

$\zeta (0)={\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \sin \left({\frac {\pi s}{2}}\right)\ \zeta (1-s)=$

${\frac {1}{\pi }}\lim _{s\rightarrow 0}\ \left({\frac {\pi s}{2}}-{\frac {\pi ^{3}s^{3}}{48}}+...\right)\ \left(-{\frac {1}{s}}+...\right)=-{\frac {1}{2}}\!$

u kojoj je funkcija definisana, gdje red divergira po analitičkom produženju. U tom smislu vrijedi 1 + 1 + 1 + 1 + · · · = ζ(0) = −¹⁄₂.

Može se reći da je

$\sum _{n=1}^{m}n^{0}=m$

Lako se dokazuje matematičkom indukcijom.

$\sum _{n=1}^{1}n^{0}=1^{0}=1$

$\sum _{n=1}^{2}n^{0}=1^{0}+2^{0}=1+1=2$

$\sum _{n=1}^{3}n^{0}=1^{0}+2^{0}+3^{0}=1+1+1=3$

$\sum _{n=1}^{4}n^{0}=1^{0}+2^{0}+3^{0}+4^{0}=1+1+1+1=4$

${\frac {n^{m}}{n^{m}}}=n^{m-m}=n^{0}=1$ Tvrdnja ne važi za $n=0$ jer $0^{0}$ nema smisla

U Dekartovom koordinantnom sistemu

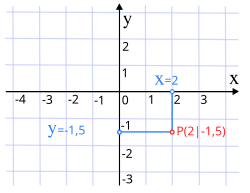
Dekartov koordinantni sistem

U Dekartovom koordinantnom sistemu funkcija $\ f(x)=\sum _{n=1}^{x}n^{0}$ sadrži iste tačke kao funkcija $\ f(x)=x$

Za $\ x>0$

Funkcija $\ f(x)=k\sum _{n=1}^{x}n^{0}$ predstavlja linije u I kvadrantu za ${\displaystyle$ :\ k\geq 0}

Funkcija $\ f(x)=k\sum _{n=1}^{x}n^{0}$ predstavlja linije u IV kvadrantu za $\ k\leq 0$ .

Za $x<0$:

Funkcija $\ f(x)=k\sum _{n=1}^{-x}n^{0}$ predstavlja linije u II kvadrantu $\ k\geq 0$ .

Funkcija $\ f(x)=k\sum _{n=1}^{-x}n^{0}$ predstavlja linije u III kvadrantu za $\ k\leq 0$ .

Demonstracija zbira

Carl Friedrich Gauss, otkrio trouglaste brojeve

$\sum _{n=1}^{m}n^{0}=\sum _{n=1}^{m}n-\sum _{n=0}^{m-1}n$

$\sum _{n=1}^{m}n^{0}=m$

$\sum _{n=1}^{m}n={\frac {m(m+1)}{2}}$

$\sum _{n=0}^{m-1}n={\frac {m(m-1)}{2}}$

$\sum _{n=1}^{m}n^{0}={\frac {m(m+1)}{2}}-{\frac {m(m-1)}{2}}={\frac {m}{2}}(m+1-m+1)={\frac {m}{2}}(2)=m$

${\frac {m(m+1)}{2}}={\binom {m+1}{2}}$ što je trouglasti broj koji je otkrio Gauss.

Formule

Razlika između zbirova

$\sum _{n=1}^{m}n-\sum _{n=1}^{m}n^{0}=\sum _{n=0}^{m-1}n$

Za $\ m=1,2$

$\ m=1$

$\sum _{n=1}^{1}n-\sum _{n=1}^{1}n^{0}=\sum _{n=0}^{0}n$ koji odgovara

$\sum _{n=1}^{1}1-\sum _{n=1}^{1}1=\sum _{n=0}^{0}0=1-1=0$ što znači $\ 0=0$

$\ m=2$

$\sum _{n=1}^{2}n-\sum _{n=1}^{2}n^{0}=\sum _{n=0}^{1}n$ koji odgovara

$\sum _{n=1}^{2}1+2-\sum _{n=1}^{2}2=\sum _{n=0}^{1}1=3-2=1$ što znači $\ 1=1$

Formule koje se odnose na razliku

$\sum _{n=1}^{m}n^{0}=\sum _{n=1}^{m}n-\sum _{n=0}^{m-1}n$

možemo dobiti slične

$\sum _{n=1}^{m}n^{0}=\sum _{n=0}^{m-1}n-\sum _{n=-1}^{m-2}n$

$\sum _{n=1}^{m}n^{0}=\sum _{n=-1}^{m-2}n-\sum _{n=-2}^{m-3}n$

$\sum _{n=1}^{m}n^{0}=\sum _{n=-2}^{m-3}n-\sum _{n=-3}^{m-4}n$

za $\ m=1,2$:

$\sum _{n=1}^{1}n^{0}=\sum _{n=0}^{0}n-\sum _{n=-1}^{-1}n=\sum _{n=1}^{1}1=\sum _{n=0}^{0}0-\sum _{n=-1}^{-1}-1$ što znači $\ 1=0+1$ odnosno $\ 1=1$ .

$\sum _{n=1}^{2}n^{0}=\sum _{n=0}^{1}n-\sum _{n=-1}^{0}n=\sum _{n=1}^{1}2=\sum _{n=0}^{2}1-\sum _{n=-1}^{0}-1$ što znači $\ 2=1+1$ odnosno $\ 2=2$

$\sum _{n=1}^{1}n^{0}=\sum _{n=-1}^{-1}n-\sum _{n=-2}^{-2}n=\sum _{n=1}^{1}1=\sum _{n=-1}^{-1}-1-\sum _{n=-2}^{-2}-2$ što znači $\ 1=-1+2$ odnosno $\ 1=1.$

$\sum _{n=1}^{2}n^{0}=\sum _{n=-1}^{0}n-\sum _{n=-2}^{-1}n=\sum _{n=1}^{2}2=\sum _{n=-1}^{0}-1-\sum _{n=-2}^{-1}-3$ što znači $\ 2=-1+3$ odnosno $\ 2=2$ .

$\sum _{n=1}^{1}n^{0}=\sum _{n=-2}^{-2}n-\sum _{n=-3}^{-3}n=\sum _{n=1}^{1}1=\sum _{n=-2}^{-2}-2-\sum _{n=-3}^{-3}-3$ što znači $\ 1=-2+3$ odnosno $\ 1=1$

$\sum _{n=1}^{2}n^{0}=\sum _{n=-2}^{-1}n-\sum _{n=-3}^{-2}n=\sum _{n=1}^{2}2=\sum _{n=-2}^{-1}-3-\sum _{n=-3}^{-2}-5$ što znači $\ 2=-3+5$ odnosno a $\ 2=2$

Opšta formula koja se odnosi na razliku

$\sum _{n=1}^{m}n^{0}=\sum _{n=-k+1}^{m-k}n-\sum _{n=-k}^{m-(k+1)}n$

$\ k=0,1,2,3,...$ na skupu $\mathbb {N}$.

Formule koje se odnose na proizvod

$\sum _{n=1}^{m+1}n^{0}\cdot \prod _{p=1}^{m}({\frac {p}{p+1}})=1$

$\sum _{n=1}^{m+1}n^{0}=m+1e\prod _{p=1}^{m}({\frac {p}{p+1}})={\frac {1}{m+1}}$

kad pomnožimo dobijemo $\ m+1\cdot {\frac {1}{m+1}}=1$

$\sum _{m=1}^{s}(\sum _{n=1}^{s+1}n^{0}\cdot \prod _{p=1}^{s}({\frac {p}{p+1}}))=\sum _{n=1}^{s}n^{0}$

Također pogledajte

• Grandijev red

Vanjski linkovi

• (niz A000027 u OEIS)

Izvor

• The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation/ 10.april 2010
• Cosmology: Techniques and Observations /

Ovaj članak, koji govori o matematičkoj analizi, je u začetku. Možete pomoći Wikipediji tako što ćete ga proširiti.