Riemannova zeta-funkcija
Ovaj članak ili neki od njegovih odlomaka nije dovoljno potkrijepljen izvorima (literatura, veb-sajtovi ili drugi izvori). |
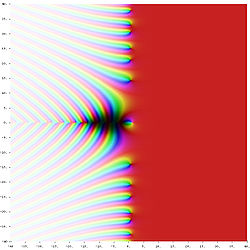
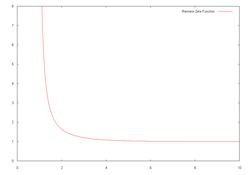
U matematici, Riemannova zeta-funkcija, nazvana po Bernhardu Riemannu, je važna funkcija u teoriji brojeva zbog veze s teoremom o raspodjeli prostih brojeva. Također se primjenjuje u fizici, teoriji vjerovanoće, i primjenjenoj statistici.
Definicija[uredi | uredi izvor]
Funkcija ζ(s) je funkcija kompleksne varijable s i najprije se definirala slijedećom beskonačnom sumom:
Leonhard Euler je otkrio vezu zeta-funkcije i raspodjele prostih brojeva
gdje, po definiciji, lijeva strana je ζ(s) a beskonačni produkt na desnoj strani je po svim prostim brojevima p.
Zeta-funkcija daje sljedeće vrijednosti za neke odabrane brojeve:
- ; (harmonički niz)
- ; koristi se za računanje kritične temperature Bose–Einsteinovog kondenzata u fizici.
- ; dokaz ove jednakosti je tzv. Bazelski problem.
- ; tzv. Apéryjeva konstanta
Poznato je da zeta-funkcija ima nule -2, -4, -6... One se nazivaju trivijalnima. Hipoteza da sve ostale (kompleksne) nule imaju realni dio jednak 1/2 je poznata kao Riemannova hipoteza i do sada nije riješena.
Također pogledajte[uredi | uredi izvor]
Literatura[uredi | uredi izvor]
- Bernhard Riemann, Über die Anzahl der Primzahlen unter einer gegebenen Grösse (1859). In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953).
- Jacques Hadamard, Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques, Bulletin de la Societé Mathématique de France 14 (1896) pp 199–220.
- Helmut Hasse, Ein Summierungsverfahren für die Riemannsche ζ-Reihe, (1930) Math. Z. 32 pp 458–464. (Globally convergent series expression.)
- E. T. Whittaker and G. N. Watson (1927). A Course in Modern Analysis, fourth edition, Cambridge University Press (Chapter XIII).
Vanjski linkovi[uredi | uredi izvor]
- Riemann Zeta Function, in Wolfram Mathworld - objašnjenje koje koristi matematički pristup (eng.)
- Tablica odabranih nula Arhivirano 17. 5. 2009. na Wayback Machine
- [1] Arhivirano 29. 9. 2007. na Wayback Machine(!! kliknite na tipku on Download Now...!!) Spis sadrži 1.000.000 nula
- Prime Numbers Get Hitched općenito o važnosti prostih brojeva, za nestručnu publiku (eng.)
| Commons ima datoteke na temu: Riemannova zeta-funkcija |












