Kupa (geometrija)

Opći konus

Rotacioni konus (lijevo) i kosi konus (desno).

Konus je oblo geometrijsko tijelo, koje nastane kao presjek konusnog prostora i sloja ravni.

Dio konusnog prostora, koji tvori površinu konus naziva se omotač ili plašt konusa. Ravni rez konusnog prostora koji graniči sa slojem ravni naziva se osnova. Tačka, u kojoj se rez ravni reducira u tačku se naziva vrh konusa. Okomita udaljenost između baze i vrha se naziva visina konusa. Udaljenost između baze i vrha konusa, po omotaču se naziva ivica konusa.

Ako je baza konusa krug, onda je to kružni konus. Ako okomica iz vrha na ravan baze prolazi sredinom baze kružnog konusa, to je rotacioni konus ili. Ako je kružni konus neokomit onda se naziva kosi.

Konusni prostor

Konusni prostor

Neka imamo zatvorenu krivu $k$, koja leži u ravni. tačke, koje pripadaju pravoj koja prolazi proizvoljnom tačkom krive $k$ i vrhom $V$ koji leži van krive $k$ čini konusovu oblast. Dio prostora omeđena konusovom oblasti se zove konusovi prostor.

Konusova oblast je skup tačaka u prostoru, koja nastane iz konusa tako, što se odstrani baza konusa i svaka duž omotača produži na pravu.

Jednačine

Konusna oblast (kvadratni konus) s vrhom u početku, koja u ravni $z=c$ prolazi elipsom ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$, ima jednačinu

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=0$

Ta oblast je asimptotska oblast (asimptotski konus) hiperboloida

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=\pm 1$

Za $a=b$ radi se o rotacionom konusu sa osom rotacije $z$.

Konusova oblast sa vrhom u tački $[x_{0},y_{0},z_{0}]$ je moguće izraziti jednačinom

$F\left({\frac {x-x_{0}}{z-z_{0}}},{\frac {y-y_{0}}{z-z_{0}}}\right)=0$

Osobine

Za volumen konusa vrijedi

$V={\frac {1}{3}}\cdot S_{p}\cdot h$,

gdje $S_{p}$ je površina baze a $h$ je visina konusa.

Rotacioni konus

Rotacioni konus

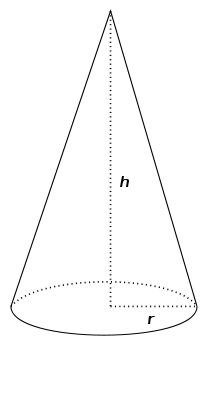
Rotacioni konus je rotaciono tijelo nastalo obrtanjem pravouglog trougla u prostoru oko jedne od kateta. Obrtanjem druge katete nastane baza konusa, obrtanjem hipotenuze nastane omotač konusa. U osnovi omotač konusa je "smotani" kružni isječak. Zajednička tačka ose rotacije i hipotenuze je vrh konusa.

Konusni presjeci

Sa geometrijskog stajališta konusni presjeci su nastali presjekom konusove površi i neke ravni. Razlikujemo:

Singularni rez konusa – ako ravan reza prolazi vrhom konusa, mogu nastati tri slučaja:

• presjek je tačka (vrh konusa), ako je ugao, kojeg ravan reza zaklapa s osom konusa, veći nego ugao, kojeg obrazuju prave konusnog položaja sa konusnom osom
• presjek je prava koja leži na konusovoj površi, ako je ugao, kojeg ravan reza zaklapa sa osom konusa jednak uglu, kojeg obrazuju prave konusnog položaja sa konusnom osom
• presjek su dvije prave, koje prolaze vrhom konusa, ako je ugao, kojeg ravan reza zaklapa sa osom konusa, manji nego ugao, kojeg obrazuju prave konusnog položaja sa konusnom osom

Regularni rez konusa - ako ravan reza ne prolazi vrhom konusa, mogu nastati četiri slučaja:

• presjek je kružnica, ako ravan reza okomita na osu konusa
• presjek je elipsa, ako je ugao, kojeg ravan reza obrazuje sa osom konusa, veći nego ugao, kojeg obrazuju prave konusnog položaja sa konusnom osom, ali ravan reza nije okomita na osu konusa
• presjek je parabola, ako je ugao, kojeg ravan reza zaklapa sa osom konusa jednak uglu, kojeg obrazuju prave konusnog položaja sa konusnom osom
• presjek je hiperbola, koje prolaze vrhom konusa, ako je ugao, kojeg ravan reza zaklapa sa osom konusa, manji nego ugao, kojeg obrazuju prave konusnog položaja sa konusnom osom

Također pogledajte

• Demokrit

Vanjski linkovi

• Kupa (geometrija) na Wikimedia Commonsu