Paralelogram

Paralelogram.

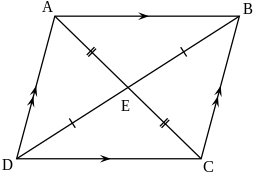
Paralelogram je četverougao koji se sastoji od dva para paralelnih i sukladnih suprotnih stranica. Odnosno to je presjek dvije pruge. Naspramni ugalovi su također jednaki Dijagonale, koje označavamo sa e i f, se polove. Presjek dijagonala je sredina svake dijagonale.

Definicija 1

Paralelogram je centralno simetričan četverougao kome je centar simetrije presječna tačka dijagonala.

Teorema 1

Paralelogram ima ove osobine

• on je centralno simetričan četverougao
• dijagonale mu se polove
• naspramne stranice su mu jednake
• naspramni uglovi su mu jednaki
• susjedni uglovi su mu suplementni

Teorema 2

Četverougao sa osobinama

• centralno simetrična je figura
• dijagonale mu se polove
• naspramne stranice su mu jednake
• naspramni uglovi su mu jednaki
• susjedni uglovi su mu suplementni
• naspramne stranice su mu jednake i paralelne

je paralelogram

Vrste

Romb - sve su stranice jednake dužine.
Pravougaonik - svi su uglovi i pravi (naspramne stranice jednake.
Kvadrat – pravougaonik koji ima jednake dužine stranica i sve su uglove prave.

Formule

Površina P =$a\cdot \;h_a$ ili P =$b\cdot \;h_b$

Obim O = 2(a+b)

Radijus upisane kružnica|kružnice r = $\frac{h_a}{2}$