Pascalov trougao

Svaki broj u Pascalovom trouglu je suma dva susjedna broja u redu iznad njega.

Pascalov trougao je termin prema autoru djela Traité du triangle arithmétique (Rasprava o aritmetičkom trouglu) koje je objavljena posthumno u 1665. U njemu je Pascal prikupio nekoliko ondašnjih znalaca o trokutu i zaposlio ih na rješavanju problema u teoriji vjerovatnoće. Trougao je po Pascalu kasnije nazvao Pierre Raymond de Montmort (1708.), koji je pod nazivom "Table de M. Pascal pour les combinaisons" (francuski: Tabela gospodina Pascal za kombinacije) i Abraham de Moivre (1730.), koji je pod nazivom "Triangulum Arithmeticum PASCALIANUM", koji je postao moderni oblik zapadnjačkog imena.^[1]

U matematici, Pascalov trougao je tako uobličeni niz binomnih koeficijenta, tj. trougao od niza ekspanzije binoma (1 + 1)ⁿ. U zapadnom svijetu ga je imenovao francuski matematičar Blaise Pascal, iako su ga drugi matematičari studirli stoljećima prije njega u Indiji.^[2] Iranu, Kini, Njemačkoj i Italiji.^[3]

Redovi Pascalovog trougla su konvencionalno poredani počevši od reda n = 0 na vrhu. Svi unosi u svakom redu su numerirani na lijevoj strani, uz početak sa k = 0 i obično približeni brojevima u odgovarajućem redu. Jednostavna konstrukcija trougla ide slijedećim tokom. Na redu 0, upiše se samo broj 1. Za konstrukciji elemenata slijedećih redova slijedi model: svaki red počinje brojem 1, koji se upisuje jedno mjesto ispred 1 prethodnog reda, a naredni broj se dobija zbrajanjem dva susjedna iz prethodnog. Na primjer, prvi broj u prvom redu je 1 (zbir 0 i 1), dok su brojevi 1 i 3 u trećem redu dodaju da proizvedu broj 4 u četvrtom redu.

(x+y)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}y^{k}

,

onda

{n \choose k}={n-1 \choose k-1}+{n-1 \choose k}

za bilo koju ne-negativni cijeli broj n i bilo cijeli K između 0 i n .^[4] Pascalov trougao ima višedimenziske generalizacije. Trodimenzijska verzija se zove Pascalova piramida ili Pascalov tetraedar, dok je opšta verzije nazivaju Pascalove jednadžbe.

Potencije broja 2[uredi | uredi izvor]

Zbir brojeva u pojedinom redu Pascalovog trougla daje potenciju broja 2. Tako je

red jednak $1=2^{0}$
red jednak $1+1=2^{1}$
red jednak $1+2+1=2^{2}$
red jednak $1+3+3+1=2^{3}$
red jednak $1+4+6+4+1=2^{4}$
red jednak $1+5+10+10+5+1=2^{5}$

{n \choose 0}+{n \choose 1}+\cdots +{n \choose n-1}+{n \choose n}=2^{n}.

Potencije broja 11[uredi | uredi izvor]

Posmatramo li brojeve jednog reda kao cifre jednog broja, dolazi se do zanimljivog otkrić da se radi o potencijama broja 11. Tako je

$1=11^{0}$
$11=11^{1}$
$121=11^{2}$
$1331=11^{3}$
$14641=11^{4}$

Od šestog reda pa nadalje dvocifrene brojeve čitamo na drugi način. Kako imamo brojeve 1, 5,10, 10,5, 1 čita,o ih na sčkedeći način $1(5+1)(0+1)(0+5)051$ tj. $161051=11^{5}$

Figurativni brojevi[uredi | uredi izvor]

Stari su Grci posebnu pažnju posvečivali su figurativnim brojevima. To su brojevi koji se mogu pravilno rasporediti po stranicama i unutrašnjosti pravilnih poligona. Tako imamo trouglaste, četverouglaste, petougaone i šestougaone brojeve

Niz trougaonih brojeva nalazimo u Pascalovom trouglu do niza prirodnih brojeva. Formula opšteg člana niza je $T(n)={\frac {1}{2}}n(n+1)$

Tetraedarni brojevi 1, 4, 10, 20, 35, 56,84, predstavljaju niz parcijalnih zbirova trouglastih brojeva. U trouglu ih nalazimo na mjestu četvrte dijagonale Formula opšteg člana niza je $T(n)={\frac {1}{6}}n(n+1)(n+2)$

Geometrijski se ti brojevi mogu prikazati kao pravilno raspoređene tačke po bridovima, stranama i u unutrašnjosti tetraedra

Formula za rješenje problema ${\frac {\tbinom {2n}{n}}{n+1}}$

Binomni koeficijenti[uredi | uredi izvor]

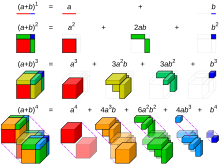
Pascalov trougao se veže uz binomni teorem. Koeficienti pojedinih redova Pascalovog trougla predstavljau binomne koeficiente. označavaju se sa ${\tbinom {n}{k}}$ , gdje je n broj reda , k broj koeficienta u redu.

Za binomne koeficijente vrijedi simetričnost tj ${\tbinom {n}{k}}={\tbinom {n}{n-k}}$ , pa su i redovi u Pascalovom trouglu simetrični.

$(x+1)^{n}=\sum _{i=0}^{n}a_{i}x^{i}.$

(x+1)^{n+1}=(x+1)(x+1)^{n}=x(x+1)^{n}+(x+1)^{n}=\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{i=0}^{n}a_{i}x^{i}.

{\begin{aligned}&\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{i=0}^{n}a_{i}x^{i}\\&{}=\sum _{i=1}^{n+1}a_{i-1}x^{i}+\sum _{i=0}^{n}a_{i}x^{i}\\&{}=\sum _{i=1}^{n}a_{i-1}x^{i}+\sum _{i=1}^{n}a_{i}x^{i}+a_{0}x^{0}+a_{n}x^{n+1}\\&{}=\sum _{i=1}^{n}(a_{i-1}+a_{i})x^{i}+a_{0}x^{0}+a_{n}x^{n+1}\\&{}=\sum _{i=1}^{n}(a_{i-1}+a_{i})x^{i}+x^{0}+x^{n+1}\end{aligned}}

Reference[uredi | uredi izvor]

^ Fowler D. "The Binomial Coefficient Function". The American Mathematical Monthly. 103 (1): 1–17. doi:10.2307/2975209. JSTOR 2975209. Zanemaren tekst "1996" (pomoć); CS1 održavanje: nepreporučeni parametar (link)
^ Maurice Winternitz M. : History of Indian Literature, Vol. III
^ Peter Fox (1998). Cambridge University Library: the great collections. Cambridge University Press. ISBN 978-0-521-62647-7. Provjerite vrijednost parametra |isbn=: invalid character (pomoć).
^ The binomial coefficient $\scriptstyle {n \choose k}$ konvencijski set za 0 ako je k isto ili manje od 0 ili veće od n.

Izvor[uredi | uredi izvor]

Pascalov ili kineski trougao Arhivirano 28. 11. 2020. na Wayback Machine

Također pogledajte[uredi | uredi izvor]

[1] Fowler D. "The Binomial Coefficient Function". The American Mathematical Monthly. 103 (1): 1–17. doi:10.2307/2975209. JSTOR 2975209. Zanemaren tekst "1996" (pomoć); CS1 održavanje: nepreporučeni parametar (link)

[2] Maurice Winternitz M. : History of Indian Literature, Vol. III

[roots-3] Peter Fox (1998). Cambridge University Library: the great collections. Cambridge University Press. ISBN 978-0-521-62647-7. Provjerite vrijednost parametra |isbn=: invalid character (pomoć).

[4] The binomial coefficient $\scriptstyle {n \choose k}$ konvencijski set za 0 ako je k isto ili manje od 0 ili veće od n.

[1]

[2]

[3]

[4]