Adijabatski proces
Ovaj članak ili neki od njegovih odlomaka nije dovoljno potkrijepljen izvorima (literatura, veb-sajtovi ili drugi izvori). |
| Termodinamika |
|---|
 |
U termodinamici, adijabatski proces ili izokalorični proces je proces u kojem nema prijenosa toplote prema ili iz fluida. Naziv "adijabatski" doslovno označava odsutnost prijenosa toplote. Na primjer, adijabatska granica je granica koja je nepropusna za prijenos toplote, te se za sistem kaže da je adijabatski (ili toplotno) izolovan - izolacijski zid aproksimira adijabatsku granicu. Drugi je primjer temperatura adijabatskog plamena, koja predstavlja temperaturu koju bi dostigao plamen u odsutnosti gubitka toplote prema okolini. Adijabatski proces, koji je povratni, se također zove izentropskim procesom.
Suprotni ekstrem - maksimalnog prijenosa toplote s okolinom, uzrokujući konstantno održavanje temperature - je poznat kao izotermni proces. Budući da je temperatura termodinamički konjugat entropije, izotermni proces je konjugat adijabatskom procesu za povratne transformacije.
Transformacija termodinamičkog sistema se može smatrati adijabatskom kada je dovoljno brza da značajna količina toplote nije izmjenjena između sistema i okoline. Adijabatski proces se, također, može zvati kvazistatičkim. Kao suprotnost, transformacija termodinamičkog sistema se može smatrati izotermnom ako je dovoljno spora da temperatura sistema ostane konstantnom izmjenom toplote s okolinom.
Adijabatsko zagrijavanje i hlađenje[uredi | uredi izvor]
Adijabatske promjene temperature dešavaju se zbog promjene pritska plina, pri čemu se ne dodaje niti oduzima ikakva toplota. U suprotnosti, slobodno širenje je izotermni proces za idealan plin.
Adijabatsko zagrijavanje dešava se kada se pritisak plina poveća od izvršenog rada od strane sredine koja ga okružuje, npr. klip. Dieselov motor se oslanja na adijabatsko zagrijavanje tokom kompresionog zamaha kako bi povisio temperaturu dovoljno da zapali gorivo.
Adijabatsko zagrijavanje, takođerm se dešava u Zemljinoj atmosferi kada se zračna masa spušta, naprimjer, katabatički vjetar ili fen koji struji nizbrdo.
Adijabatsko hlađenje dešava se kada se pritisak substance smanji u toku vršenja rada na njenu okolicu. Adijabatsko hlađenje ne mora uključivati fluid. Jedna tehnika, kojom se dostižu veoma niske temperature (hiljaditi ili čak milioniti dijelovi stepena iznad apsolutne nule), je adijabatska demagnetizacija, gdje se promjena u magnetnom polju magnetičnog materijala koristi kako bi se ostvarilo adijabatsko hlađenje. Adijabatsko hlađenje se, također, dešava u Zemljinoj atmosferi sa orografskim uzdizanjem i zavjetrinskim talasima, što može dovesti do formiranja pileusa ili lentikularnog oblaka ako se zrak ohladi ispod tačke rošenja.
Nadolazeća magma, također, prolazi kroz adijabatsko hlađenje prije erupcije.
Takve temperaturne promjene mogu se kvatifikovati koristeći zakon idealnog plina, ili hidrostatičku jednačinu za atmosferske procese.
Ni jedan proces nije idealno adijabatski. Mnogi procesi su blizu adijabatskog, te se mogu lahko aproksimirati korištenjem adijabatske pretpostavke, ali uvijek postoji neki gubitak toplote; pošto ne postoji savršeni izolator.
Idealni plin (povratni proces)[uredi | uredi izvor]
Matematička jednačina za idealni fluid koji se podvrgava povratnom (bez generacije entropije) adijabatskom procesu je
gdje je P pritisak, V specifična ili molarna zapremina, i
je specifična toplota ua konstantni pritisak, je specifična toplota za konstantnu zapreminu, γ je adijabatski indeks, i je broj stepeni slobode podijeljen sa 2 (3/2 za jednoatomne plinove, 5/2 za dvoatomne plinove).
Za jednoatomne plinove, , i za dvoatomne plinove (kao što je dušik i kiseonik, glavne komponente zraka) . Uočite da su gornje formule primjenljive samo za klasične idealne plinove, a ne za Bose-Einsteinovu ili fermionične plinove.
Za povratne adijabatske procese, također vrijedi da je
gdje je T apsolutna temperatura.
Ovo se, također, može napisati kao
Derivacija neprekidne formule[uredi | uredi izvor]
Definicija adijabatskog procesa je da je prijenos toplote ka sistemu jednak nuli, . Tada, prema prvom zakonu termodinamike,
gdje je dU promjena unutrašnje energije sistema, a δW je isvršeni rad od strane sistema. Svaki izvršeni rad (δW) mora biti izvršen na račun unutrašnje energije U, jer se toplota δQ nije dovodila iz okoline. Rad pritisak-zapremina δW vršen od strane sistema definisan je kao
Međutim, P ne ostaje konstanta tokom adijabatskog procesa, nego se mijenja zajedno sa V.
Poželjno je poznavati kako su vrijednosti dP i dV povezane jedna s drugom tokom odvijanja adijabatskog procesa. Za idealan plin, unutrašnja energija je data kao
gdje je R univerzalna plinska konstanta, a n je broj molova u sistemu (konstanta).
Diferenciranjem jednačine (3) i upotrebom zakona idealnog plina, , dobijamo
Jednačina (4) se često izražava kao , jer je .
Sada možemo jednačine (2) i (4) uvrstit u jednačinu (1), da bi dobili
jednostavnije:
te podijeliti obe strane sa PV:
Nakon integrisanja lijeve i desne strane od do V, te od do P, i zamjenom strana, respektivno,
Eksponentovanjem obe strane,
i eliminisanjem znaka minus, dobijamo
Na kraju,
i
Derivacija diskretne formule[uredi | uredi izvor]
Promjena u unutrašnjoj energiji sistema, mjerena od stanja 1 do stanja 2, jednaka je
U isto vrijeme, izvršeni rad zbog promjena u P-V odnosima, kao rezultat ovog procesa, jednak je
Pošto nama treba adijabatski proces, sljedeća jednačina mora da vrijedi
Prema prethodnoj derivaciji,
Preraspodjela jednačine (4) daje
Zamjenom u (2) daje
Integrisanjem,
Zamjenom ,
Preraspodjelom,
Korištenjem zakona o idealnom plinu i pretpostavke da imamo konstantan molarni kvantitet (što se često dešava određenim slučajevima),
Prema neprekidnoj formuli,
Ili,
Zamjenom u prethodni izraz za ,
Zamjenom ovog izraza zajedno sa (1) u (3) daje
Pojednostavljeno,
Pojednostavljeno,
Pojednostavljeno,
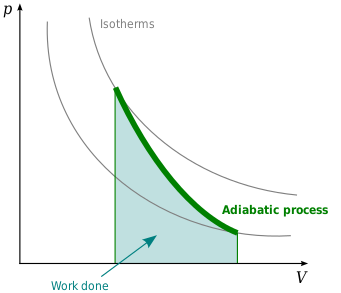
Grafici adijabata[uredi | uredi izvor]
Adijabata je kriva konstantne entropije na P-V dijagramu. Osobine adijabata na P-V dijagramu su:
- Svaka adijabata asimptotski se približava i osi V i osi P (kao i izoterma).
- Svaka adijabata presjeca svaku izotermu tačno jednom.
- Adijabata izgleda slično kao izoterma, osim što tokom ekspanzije, adijabata gubi više pritiska od izoterme, tako da ima strmiji uspun (više je vertikalna).
- Ako su izoterme konkavne prema pravcu "sjeveroistoka" (45°), tada su adijabate konkavne prema pravcu "istok-sjeveroistok" (31°).
- Ako su adijabate i izoterme predstavljene grafički pojedinačno prema tačno određenoj promjeni entropije i temperature, respektivno (kao visina na konturnoj karti), tada kako se oko kreće prema osama (prema "jugozapadu"), vidjet će se da gustoća izotermi ostaje konstantna, ali gustina adijabata se povećava. Izuzetak je neposredna blizina apsolutne nule, gdje gustoća adijabata naglo opada, te one postaju rijetke (pogledajte članak Nernstov teorem).
Sljedeći dijagram je P-V dijagram sa superpozicijama adijabata i izotermi:
Izoterme su crvene krive, a adijabate su crne krive.
Adijabate su izentropske.
Zapremina je horizontalna osa, a pritisak je vertikalna osa.
Također pogledajte[uredi | uredi izvor]
- Kružni proces
- Prvi zakon termodinamike
- Toplotni nalet
- Izobarni proces
- Izentalpijski proces
- Izentropski proces
- Izohorski proces
- Izotermni proces
- Politropski proces
- Termodinamička entropija
- Kvazistatička ravnoteža
- Ukupna temperatura zraka
- Adijabatski motor
- Magnetno rashlađivanje
Reference[uredi | uredi izvor]
- Robert J. Silbey et al. (2004). Physical chemistry. p. 55. ISBN 978-0-471-21504-2.
Vanjski linkovi[uredi | uredi izvor]
| Commons ima datoteke na temu: Adijabatski proces |































































