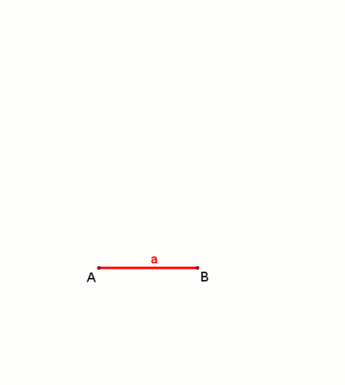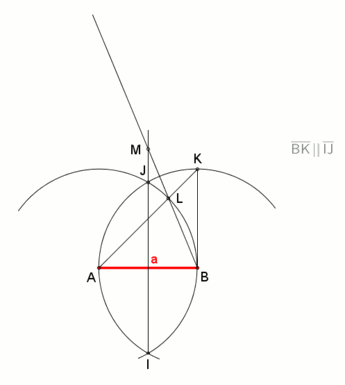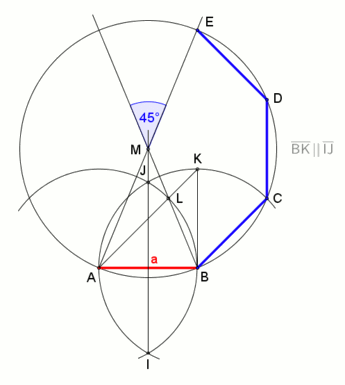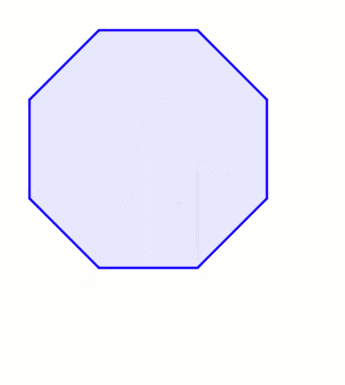
Osmougao
U geometriji, oktagon (grčki: ὀκτάγωνον – oktágōnon = osam uglova) je osmostrani poligon ili 8-ugao.
Pravilni oktogon ima Schläflijev simbol {8}[1] a može se konstruirati i kao kvaziregularni skraćeni kvadrat, t {4}, koji izmjenjuje dvije vrste bridova. Skraćeni osmerokut, t {8} je heksadekagon, {16}. 3D analog osmougla može biti rombikuboktaedar s trouglastim licima na njemu poput zamijenjenih ivica, ako se smatra da je osmerougao krnji kvadrat
Osobine općeg oktogona[uredi | uredi izvor]

Zbir svih unutrašnjih uglova bilo kojeg oktogona iznosi 1080°. Kao i kod svih poligona, vanjski uglovi iznose ukupno 360°.
Ako su kvadrati konstruirani iznutra ili sa svih strana na stranama oktogona, tada centrale tečke segmenata koji povezuju središta suprotnih kvadrata čine četverougao koji je i ekvidijagonalni i ortodijagonalni (tj. čije su dijagonale jednake dužine i pod pravim su uglom).[2]:Prop. 9
Središnji poligon referentnog oktogona ima osam vrhova u centralnim tačkama stranica referentnog oktogona. Ako su kvadrati konstruirani iznutra ili sa svih strana na stranama osmerougane središnje tačke, tada centralne tačke segmenata koji povezuju središta suprotnih kvadrata čine vrhove kvadrata.[2]
Pravilni osmerokut[uredi | uredi izvor]
Pravilni oktogon je zatvorena slika sa stranicama iste dužine i unutrašnjim uglovima iste veličine. Ima osam linija reflektivne i rotacijske simetrije reda 8. Pravilni osmerokut predstavljen je Schläflijevim simbolom {8}.
Unutrašnji ugao na svakom vrhu pravilnog oktogona je 135 ° ( radijane). Centralni ugao je 45° ( radians).
Područje[uredi | uredi izvor]
Područje pravilnog oktogona bočne dužine a dato je prema
U smislu obima R, područje
U terminu apoteme r, područje je
Ova dva potonja koeficijenta zagrađuju vrijednost pi, površine jediničnog kruga.

Područje se također može izraziti kao
gdje S = raspon oktagona ili druga najkraća dijagonala; a je dužina jedne od stranica ili osnova. To se lahko može dokazati ako se uzme osmerogao, nacrta kvadrat oko vanjske strane (pazeći da se četiri od osam stranica preklapaju sa četiri stranice kvadrata), a zatim se uzmu ugaoni trouglovi (to su 45–45–90 trouglovi) i postavljaju pod pravim uglom usmjerenim prema unutra, čineći kvadrat. Rubovi ovog kvadrata dužine su baze.
S obzirom na dužinu stranice a, raspon S
Raspon je, dakle, jednak srebrenom omjeru puta stranice, a.
Tada je područje kao gore:
U teminima raspona, posručje je:
Druga jednostavna formula za područje je
Češće je poznat raspon S , a dužinu stranice a treba odrediti, kao pri rezanju četvrtastog komada materijala u pravilni osmerougao. Iz navedenog:
Dvije krajnje dužine e, sa svake strane (dužine krakova trougala, zelene na slici, odsječene od kvadrata), kao i može se izračunati iz
Cirkumradijus i inradijus[uredi | uredi izvor]
Cirkumradijus pravilnog oktogona u smislu dužine stranice a je[3]
a inradijus :
(to je polovina srebrenom omjeru puta stranice, a ili poluraspona,S)
Dijagonale[uredi | uredi izvor]
Pravilni oktogon, u smislu dužine stranice a, ima tri različita tipa dijagonala :
- Kratka dijagonala:
- Srednja dijagonala (koja se naziva i raspon ili visina) je dvostruka dužina radijusa;
- Duga dijagonala, koja je dvostruko veća od dužine opsega.
Formula za svaku od njih slijedi iz osnovnih principa geometrije. Evo formula za njihovu dužinu:
- Kratka dijagonala: ;
- Srednja dijagonala: ( srebreni omjer puta a)
- Duga dijagonala: .
Konstrukcija i osnovna svojstva[uredi | uredi izvor]

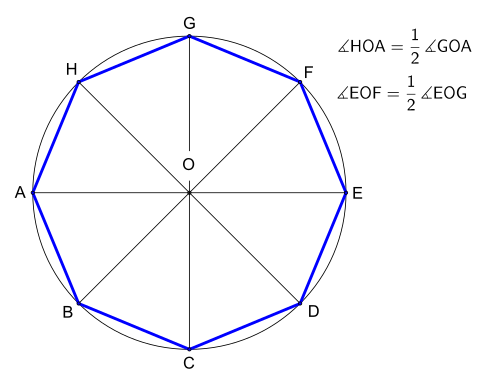
Pravilni oktagon u datom opisanom krugu može se konstruirati na sljedeći način:
- Nacrtati krug i promjer AOE, gdje je O središte, a A, E tačke na opisanoj kružnici.
- Nacrtati još jedan prečnik GOC, okomit na AOE.
- (Uzgred uočiti da su A, C, E, G vrhovi kvadrata).
- Nacrtati simetrale pravih uglova GOA i EOG, praveći još dva promjera HOD i FOB.
- A, B, C, D, E, F, G, H su tjemena oktogona.
(Konstrukcija je vrlo slična konstrukciji heksadekagona na određenoj dužini stranice.)
Pravilni osmerokut može se konstruirati pomoću ravnanjeravnanja i kompasa, kao 8 = 23, [[snaga dvojke


Pravilni osmerokut može se konstruirati pomoću Meccanoovih crtica. Potrebno je dvanaest šipki veličine 4, tri šipke veličine 5 i dvije šipke veličine 6.
Svaka strana pravilnog osmerokutu ima pola pravog ugla u središtu kruga koji povezuje njegove vrhove. Njegova površina tako se može izračunati kao zbir osam jednakokračnih trouglova, što dovodi do rezultata:
- A=Područje za oktagon sa stranicom a.
Standardne koordinate[uredi | uredi izvor]
Koordinate vrhova pravilnog oktogona usredotočenog na ishodište i dužine stranice 2 su:
- (±1, ±(1+))
- (±(1+(), ±1).
Disekcija[uredi | uredi izvor]
| 8-kubna projekcija | 24-romboidna disekcija | |
|---|---|---|

|
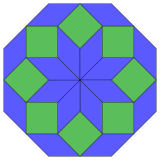 Pravilni |
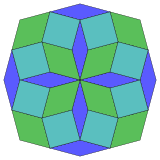 Izotoksni |
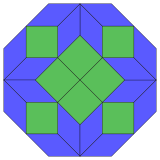
|

| |
Cokseter navodi da se svaki zonogon (gon od 2m čije su suprotne stranice paralelne i jednake dužine) može secirati na m (m –1)/2 paralelograma.[4]
To posebno vrijedi za pravilne poligone s jednako mnogo stranica, u kojemslučaju ssu vi paralelogrami rombovi. Za pravilni oktogon, m = 4, a može se podijeliti u šest rombova, s jednim primjerom prikazanim dolje. Ova razgradnja može se vidjeti kao 6 od 24 lica u Petrijevim poligonima projekcije ravni teserakt. Lista A006245 definira broj rješenja kao 8, prema 8 orijentacija ove disekcije. Ti kvadrati i rombovi koriste se u Ammann-Beenkerovim pločicama
 Teserakt |
 4 romba i 2 kvadrata |
Također pogledajte[uredi | uredi izvor]
- Trougao
- Kvadrat
- Oktogonski broj
- Oktagram
- Oktaedar, 3D oblik sa osam lica.
Reference[uredi | uredi izvor]
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, str. 9, ISBN 9780521098595.
- ^ a b Dao Thanh Oai (2015), "Equilateral triangles and Kiepert perspectors in complex numbers", Forum Geometricorum 15, 105--114. http://forumgeom.fau.edu/FG2015volume15/FG201509index.html
- ^ Weisstein, Eric. "Octagon." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Octagon.html
- ^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
Vanjski linkovi[uredi | uredi izvor]
| Potražite Osmougao na Wikirječniku, slobodnom rječniku. |
- Octagon Calculator
- Definition and properties of an octagon With interactive animation