Kosinusna teorema

Kosinusna teorema se koristi za rješavanje trougla u trigonometrijskoj ravni:

$\ a^{2}=b^{2}+c^{2}-2bc\cos \alpha ,$ gdje je α ugao nasuprot stranice a.

U sfernoj trigonometriji to je formula za rješavanje sfernog trougla:

$\cos c=\cos a\cos b+\sin a\sin b\cos C$

$\cos C=-\cos A\cos B+\sin A\sin B\cos c$

gdje je a strana nasuprot ugla A, strana b nasuprot ugla B, a strana C je nasuprot ugla C.

U ravni[uredi | uredi izvor]

U svakom trouglu je $\ a^{2}=b^{2}+c^{2}-2bc\cos \alpha ,$ gdje je ugao $\alpha$ nasuprot stranice a

$b^{2}=c^{2}+a^{2}-2ca\cos \beta$ gdje je ugao $\beta$ nasuprot stranice b

$c^{2}=a^{2}+b^{2}-2ab\cos \gamma$ gdje je ugao $\gamma$ nasuprot stranice c

Dokaz

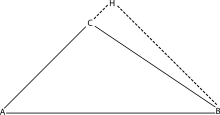
Neka je dat je oštrougli trougao ABC sa visinom CD.

Iz pravouglih trouglova BCD i ACD prema Pitagorinoj teoremi je

$a^{2}=h^{2}+(c-p)^{2},\;h^{2}=b^{2}-p^{2},$ zamjenom

$\ a^{2}=b^{2}+(c^{2}-2pc+p^{2})-p^{2},$ i

$\ a^{2}=b^{2}+c^{2}-2pc.$ pravouglog trougla ACD dobijamo

$p=b\cos \alpha ,\,$ i zamenom u prethodnu jednakost

$\ a^{2}=b^{2}+c^{2}-2bc\cos \alpha ,$

Za tupougli trougao ABC, sa uglom $\alpha$ u tjemenu A, većim od pravog ugla (90°). Visina CD = h pada na produžetak stranice AB u tačku D tako da je D-A-B, te je spoljašnji ugao CAD = 180°-α. U trouglu CAD je

DA = $\ p=b\cos(180^{o}-\alpha )=-b\cos \alpha .$

trouglovi BCD i ACD su pravougli i, prema Pitagorinoj teoremi imamo

$a^{2}=h^{2}+(c+p)^{2},\;h^{2}=b^{2}-p^{2},$

$\ a^{2}=b^{2}-p^{2}+(c^{2}+2pc+p^{2})=b^{2}+c^{2}+2pc,$

$\ a^{2}=b^{2}+c^{2}-2bc\cos \alpha ,$

Kosinusna teorema se može dokazati jednostavno i bez razmatranja različitih rasporeda koristeći vektorski račun.

${\displaystyle a^{2}={\overrightarrow {BC}}^{2}=({\overrightarrow {AC}}-{\overrightarrow {AB}})^{2}={\overrightarrow {AC}}^{2}-2{\overrightarrow {AB}}\cdot {\overrightarrow {AC}}+{\overrightarrow {AB}}^{2}=b^{2}-2bc\cos \alpha +c^{2}.}$ ( ${\displaystyle \cdot }$ skalarni proizvod.)

Na sličan način dobijamo oatale formule

Za ugao $\gamma =90^{o}=>cos90^{o}=0$ , imamo $c^{2}=a^{2}+b^{2},$ poseban slučaj kosinusne teoreme Pitagorina teorema.

Posljedice[uredi | uredi izvor]

Kvadrat bilo koje stranice trougla manji je, jednak ili veći od zbira kvadrata ostale dvije stranice, zavisno da li je suprotni ugao oštar, prav ili tup.

Dokaz:

Ako je $\alpha <90^{o},\,$ onda je $\cos \alpha >0\,$ i $a^{2}=a^{2}+b^{2}-2ab\cos \alpha <b^{2}+c^{2}.\,$

Ako je $\alpha =90^{o},\,$ onda је $\cos \alpha =0\,$ i $c^{2}=a^{2}+b^{2}.\,$

Аkо је $\alpha >90^{o},\,$ ondа је $\cos \alpha <0\,$ i $a^{2}=a^{2}+b^{2}-2ab\cos \alpha >b^{2}+c^{2}.\,$

Važi i obrnuta teorema

Теоrеmа:

Ugao trougla је оštar, рrаv, ili tup zavisno od toga da li je kvadrat suprotne stranice trougla redom je manji, jednak ili veći od zbira kvadrata ostale dvije stranice.

Dokaz:

Ako је $a^{2}<b^{2}+c^{2},\,$ onda je $\cos \alpha >0,\,$ prema tome je $\alpha <90^{o}.\,$

Аko је $a^{2}=b^{2}+c^{2},\,$ onda je $\cos \alpha =0,\,$ tј. $\alpha =90^{o}.\,$

Ako је $a^{2}>b^{2}+c^{2},\,$ onda је $\cos \alpha <0,\,$ tј. $\alpha >90^{o}.\,$

U bilo kojem paralelogramu zbir kvadrata dijagonala jednak je zbiru kvadrata sve četiri njegove strane.

${\overline {AC}}^{2}+{\overline {BD}}^{2}=2{\overline {AB}}^{2}+2{\overline {BC}}^{2}.$

${\overline {BD}}^{2}={\overline {AD}}^{2}+{\overline {AB}}^{2}-2{\overline {AB}}\cdot {\overline {AD}}\cdot \cos \alpha ,$

${\overline {AC}}^{2}={\overline {AB}}^{2}+{\overline {BC}}^{2}-2{\overline {AB}}\cdot {\overline {BC}}\cdot \cos(180^{o}-\alpha )$

$={\overline {AB}}^{2}+{\overline {BC}}^{2}+2{\overline {AB}}\cdot {\overline {AD}}\cos \alpha ,$ јер је ${\overline {BC}}={\overline {AD}}.$

Sabiranjem dobijamo

${\overline {AC}}^{2}+{\overline {BD}}^{2}=2{\overline {AB}}^{2}+2{\overline {BC}}^{2},$

Korištenje teoreme[uredi | uredi izvor]

Teoremu koristimo za rješavanje trougla

ako znamo dvije stranice i ugao naspram tražene stranice

$\,c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;$

Uglove trougla ako znamo sve tri stranice

$\,\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;$

Treča stranica ako znamo dvije stranice i ugao naspram jedne od njih

$\,a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.$ Ako se radi pravouglom trouglu koristi se Pitagorina teorema

Koristeći Pitagorin teorem[uredi | uredi izvor]

Tupi ugao[uredi | uredi izvor]

Teoremu dokazuje Euklid pomoću Pitagorinu teoremu

$c^{2}=(b+d)^{2}+h^{2},\,$

$d^{2}+h^{2}=a^{2}.\,$

$c^{2}=b^{2}+2bd+d^{2}+h^{2}.\,$

$c^{2}=a^{2}+b^{2}+2bd.\,$ ^[1]

d=a\cos(\pi -\gamma )=-a\cos \gamma .\,

Oštri ugao[uredi | uredi izvor]

${\begin{aligned}c^{2}&{}=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&{}=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&{}=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}$

$\cos ^{2}\gamma +\sin ^{2}\gamma =1.\,$

Koristeći Ptolomejevu teoremu[uredi | uredi izvor]

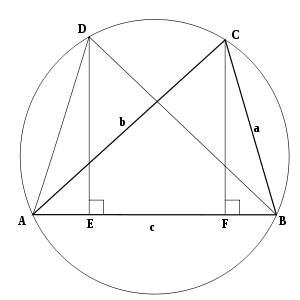
${\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}$

${\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}$