Fraktal
Ovaj članak ili neki od njegovih odlomaka nije dovoljno potkrijepljen izvorima (literatura, veb-sajtovi ili drugi izvori). |

Fraktali su geometrijski objekti čija je fraktalna dimenzija strogo veća od topološke dimenzije. Drugim riječima, to su objekti koji daju jednak nivo detalja nezavisno od rezolucije koja se koristi. Fraktale je moguće uvećavati beskonačno mnogo, a da se pri svakom novom povećanju vide neki detalji koji prije povećanja nisu bili vidljivi i da količina novih detalja uvijek bude otprilike jednaka. Oni su (barem približno) međusobno samoslični (sastoje se od umanjenih verzija samih sebe), ali isuviše nepravilni da bi se opisali jednostavnom geometrijom. Tako npr. dužina nije fraktal, iako je samoslična (sastoji se od beskonačno mnogo dužina, a sve dužine su slične). Laički rečeno, oni su "načičkani" do u beskonačnost.
Osnove[uredi | uredi izvor]


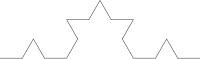

Kao jedan od najjednostavnijih i najpoznatijih primjera fraktala je Kochova krivulja. Ona se dobija tako da se dužina zamijeni likom prikazanim na prvoj slici lijevo. To se naziva prvom iteracijom Kochove krivulje. Druga iteracija dobije se tako da se svaka od četiri dužine iz prve iteracije zamijeni istim likom. Za treću iteraciju mora se zamijeniti svaka od 16 dužina itd. Kochova krivulja se dobije nakon beskonačnog broja iteracija. Na donjoj slici desno vidi se svojstvo samosličnosti, svaki dio Kochove krivulje je sličan cijeloj krivoj.
Još jedan jednostavan primjer je trougao Sierpińskog. Kreće se od trougla (nulta iteracija) koji se zamijeni trima trouglima upola manje dužine stranice (prva iteracija). Sa svakim trouglom postupak se ponovi (druga iteracija) i tako u beskonačnost.

Fraktalna dimenzija[uredi | uredi izvor]

Nakon velikog broja iteracija može se vidjeti da dužina Kochove krivulje teži u beskonačnost kad broj iteracija teži u beskonačnost. Međutim, cijela ta dužina je i dalje na istoj površini, samo je "zgužvana". Stepen te "zgužvanosti" može se vidjeti iz fraktalne dimenzije. Drugim riječima, ona daje uvid u to u kojoj mjeri neki fraktal zauzima ravan (ili općenito n-dimenzionalni prostor u kojem se nalazi). Tako Kochova krivulja ima fraktalnu dimenziju približno 1,2619, a tepih Sierpińskog približno 1,8928. Iz vrijednosti, kao i iz slika, može se vidjeti da je tepih Sierpińskog "gušći", "načičkaniji" od Kochove krivulje, odnosno ispunjava veći dio ravni.
Podjela[uredi | uredi izvor]
Postoje razni načini klasifikacije fraktala. Jedan od načina je svrstati ih po stepenu samosličnosti. Potpuno samoslični fraktali su oni koji sadrže kopije sebe koje su slične cijelom fraktalu. Primjeri su svi geometrijski fraktali, npr. trougao Sierpińskog, Kochova krivulja, Hilbertova krivulja, Cantorov skup itd. Ako fraktal sadrži male kopije sebe koje nisu slične cijelom fraktalu, nego se pojavljuju u iskrivljenom obliku, govori se o kvazi samosličnom fraktalu (Mandelbrotov i Julijin skup i sl.). Moguće je i da fraktal ne sadrži kopije samog sebe, ali da neke njegove osobine (npr. fraktalna dimenzija) ostaju iste pri različitim mjerilima. U tom slučaju govori se o statističkoj samosličnosti, a tipičan primjer je Perlinov šum.
Fraktale je moguće klasificirati i po načinu njihovog nastanka. Sistemi iteriranih funkcija (Iterated Function Systems – IFS) nastaju kopiranjem te homotetijom, rotiranjem i/ili translacijom kopije te mogućim zamjenjivanjem nekog elementa kopijom. Fraktali definisani rekurzivnim relacijama određeni su rekurzivnom matematičkom formulom koja određuje pripada li određena tačka prostora (npr. kompleksne ravni) skupu ili ne. Slučajni fraktali nastaju crtanjem grafova nekih stohastičnih procesa, npr. Brownovog kretanja. Zanimljivo je da i prva i druga podjela daje isti rezultat, sistemi iteriranih funkcija daju potpuno samoslične fraktale, fraktali definirani rekurzivnim relacijama su kvazi samoslični, a slučajni fraktali su samo statistički samoslični. Zbog jednostavnosti, za te tri grupe koriste se redom nazivi: geometrijski, algebarski i stohastični fraktali.
- geometrijski fraktali
- na pravcu
- u ravni
- u trodimenzionalnom prostoru
- analogoni nižedimenzionalnim fraktalima
- Oktaedarski fraktal
- Dodekaedarski fraktal
- Ikosaedarski fraktal
- algebarski fraktali
- stohastični fraktali
Primjena[uredi | uredi izvor]


Najjednostavniji primjer primjene fraktala u računarskoj grafici jeste stvaranje terena, posebno planina. Planina se izrađuje tako da se horizontalno položenom trouglu svaki vrh povisi ili snizi za slučajno odabranu vrijednost. Tako dobijenom trouglu spoje se polovišta stranica te se tako dobijaju četiri nova trougla. Srednjem od njih (omeđen trima dužinama koje spajaju polovišta stranica prvobitnog trougla) povisuju se ili snižavaju vrhovi kao i početnom trouglu, ali se koriste dvostruko manje vrijednosti. Postupak se zatim ponavlja za sva četiri trougla. Planine se mogu napraviti i na drugi način, pomoću Perlinovog šuma.

Pomoću sistema iteriranih funkcija u tri dimenzije moguće je kreirati raznoliko rastinje: grmove, drveće, busene trave i sl. Ako se isto napravi u trodimenzionalnom sistemu te na kraj svake "grančice" se doda list, rezultati mogu biti zapanjujuće slični stvarnim pojavama u prirodi.
Nadalje, fraktali se koriste i u kompresiji podataka. Od manje važnih primjena tu je (naravno, vrlo ograničeno) predviđanje nekih stohastičkih procesa kao što su potresi; slaganje snopova optičkih vlakana, oponašanje rada neuronskih mreža za razvoj umjetne inteligencije itd. Za male uređaje kao što su mobiteli proizvode se antene u obliku fraktala koje zbog toga mogu koristiti širok spektar frekvencija ne zauzimajući mnogo mjesta. Uzorak za vojnu kamuflažnu odjeću koristi fraktalnu strukturu koja se nigdje ne ponavlja te se stoga mnogo teže primjećuje u prirodi, gdje ništa nije matematički pravilno. Provode se istraživanja za liječenje aritmije srca, gdje srce kuca u haotičnom režimu. Vanjskom stimulacijom srca pokušava se postići prijelaz u pravilan režim. Na kraju, neke fraktalne strukture su izrazito lijepe pa se prezentiraju kao umjetnička djela.
Fraktali u prirodi[uredi | uredi izvor]


Mogućnost primjene fraktala leži u činjenici da mnogi od njih sliče prirodnim pojavama. Često se kao primjer spominje posebna vrsta brokule te paprat. Med kristalizira u fraktalne oblike, a drveće je, kao i paprat, po svojoj prirodi fraktalnih svojstava (deblo se grana na grane koje se granaju na grančice...). Zapravo, na neki način gotovo cijeli svijet je sačinjen od fraktalnih oblika. Mandelbrot je koristio primjer obale mora kao fraktal: uvale sliče zalivima, hrtovi poluostrva i slično. Kad bismo se malo približili[ko?], svaka stijena bi sličila poluostrvu. Veće približavanje otkriva izbočine u stijeni koje također podsjećaju na poluostrva. U tim izbočinama postoje sitne udubine koje imaju isti oblik kao i zalivi. Takav postupak se može nastaviti sve do molekulskih razmjera. Mnogo dijelova ljudskog tijela je fraktalne strukture. Očit primjer je sistem krvnih žila, koje u principu imaju istu strukturu kao i drveće. DNK se namota dajući fraktalnu strukturu.
Također pogledajte[uredi | uredi izvor]
- Teorija haosa
- Topološka dimenzija
- Fraktalna dimenzija
- Sistemi iteriranih funkcija (IFS)
- Lindenmayerov sistem
- T-linijar (fraktal)
Vanjski linkovi[uredi | uredi izvor]
| Fractal na Wikimedia Commonsu. |

