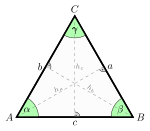
Jednakostraničan trougao je trougao u kojem su sve tri stranice jednake
malo
A
B
=
B
C
=
A
C
=>
a
=
b
=
c
{\displaystyle AB=BC=AC=>a=b=c}
i sva tri ugla jednaka
α
=
β
=
γ
=
π
3
=
60
∘
{\displaystyle \alpha =\beta =\gamma ={\frac {\pi }{3}}=60^{\circ }}
Presjek težišnih duži (
T
{\displaystyle T}
visina (
H
{\displaystyle H}
O
{\displaystyle O}
O
{\displaystyle O}
Težišne duži su međusobno jednake.
t
a
=
t
b
=
t
c
{\displaystyle t_{a}=t_{b}=t_{c}}
Visine su međusobno jednake.
h
a
=
h
b
=
h
c
{\displaystyle h_{a}=h_{b}=h_{c}}
Težišne duži su podudarne visinama. Također, težišne duži su podudarne simetralama uglova i stranica.
h
≅
t
{\displaystyle h\cong t\,}
Veličine izražene preko stranice tougla
površina
P
=
a
2
3
4
{\displaystyle P={\frac {a^{2}{\sqrt {3}}}{4}}}
obim
O
=
3
a
{\displaystyle O=3a\,\!}
poluprečnik opisane kružnice
R
=
a
3
{\displaystyle R={\frac {a}{\sqrt {3}}}}
poluprečnik upisane kružnice
r
=
3
6
a
{\displaystyle r={\frac {\sqrt {3}}{6}}a}
r
=
R
2
{\displaystyle r={\frac {R}{2}}}
visina
h
=
3
2
a
{\displaystyle h={\frac {\sqrt {3}}{2}}a}
Ove veličine možemo izraziti i preko visine
P
=
h
2
3
{\displaystyle P={\frac {h^{2}}{\sqrt {3}}}}
R
=
2
h
3
{\displaystyle R={\frac {2h}{3}}}
r
=
h
3
{\displaystyle r={\frac {h}{3}}}
Visinu je moguće izračunati pomoću jedne od dvije formule:
h
=
a
⋅
3
2
{\displaystyle h={\frac {a\cdot {\sqrt[{}]{3}}}{2}}}
P
=
h
2
⋅
3
3
{\displaystyle P={\frac {h^{2}\cdot {\sqrt[{}]{3}}}{3}}}
h
=
3
P
3
{\displaystyle h={\sqrt[{}]{\frac {3P}{\sqrt[{}]{3}}}}}
kada se racionališe i skrati dobija se
h
=
3
P
3
3
=
P
3
{\displaystyle h={\sqrt[{}]{\frac {3P\,{\sqrt[{}]{3}}}{3}}}={\sqrt[{}]{{P}\,{\sqrt[{}]{3}}}}}
Neka je dat trougao
A
B
C
{\displaystyle ABC}
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
s
{\displaystyle s}
R
{\displaystyle R}
r
{\displaystyle r}
[1]
Trougao je jednakostraničan ako i samo ako je bilo koja od sljedečih izjava tačna.
Stranice
a
=
b
=
c
{\displaystyle \displaystyle a=b=c}
a
2
+
b
2
+
c
2
=
a
b
+
b
c
+
c
a
{\displaystyle \displaystyle a^{2}+b^{2}+c^{2}=ab+bc+ca}
a
b
c
=
(
a
+
b
−
c
)
(
a
−
b
+
c
)
(
−
a
+
b
+
c
)
{\displaystyle \displaystyle abc=(a+b-c)(a-b+c)(-a+b+c)}
1
a
+
1
b
+
1
c
=
25
R
r
−
2
r
2
4
R
r
{\displaystyle \displaystyle {\frac {1}{a}}+{\frac {1}{b}}+{\frac {1}{c}}={\frac {\sqrt {25Rr-2r^{2}}}{4Rr}}}
Poluobim
s
=
2
R
+
(
3
3
−
4
)
r
{\displaystyle \displaystyle s=2R+(3{\sqrt {3}}-4)r}
s
2
=
3
r
2
+
12
R
r
{\displaystyle \displaystyle s^{2}=3r^{2}+12Rr}
s
=
3
3
r
{\displaystyle \displaystyle s=3{\sqrt {3}}r}
s
=
3
3
2
R
{\displaystyle \displaystyle s={\frac {3{\sqrt {3}}}{2}}R}
Uglovi
α
=
β
=
γ
=
π
3
=
60
∘
{\displaystyle \alpha =\beta =\gamma ={\frac {\pi }{3}}=60^{\circ }}
cos
α
+
cos
β
+
cos
γ
=
3
2
{\displaystyle \displaystyle \cos {\alpha }+\cos {\beta }+\cos {\gamma }={\frac {3}{2}}}
sin
α
2
sin
β
2
sin
γ
2
=
1
8
{\displaystyle \displaystyle \sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}={\frac {1}{8}}}
Površina
P
=
a
2
+
b
2
+
c
2
4
3
{\displaystyle \displaystyle P={\frac {a^{2}+b^{2}+c^{2}}{4{\sqrt {3}}}}}
P
=
3
4
(
a
b
c
)
2
3
{\displaystyle \displaystyle P={\frac {\sqrt {3}}{4}}(abc)^{^{\frac {2}{3}}}}
Poluprečnik opisane i upisane kružnice
R
=
2
r
{\displaystyle \displaystyle R=2r}
9
R
2
=
a
2
+
b
2
+
c
2
{\displaystyle \displaystyle 9R^{2}=a^{2}+b^{2}+c^{2}}
r
=
r
a
+
r
b
+
r
c
9
{\displaystyle \displaystyle r={\frac {r_{a}+r_{b}+r_{c}}{9}}}
r
a
=
r
b
=
r
c
{\displaystyle \displaystyle r_{a}=r_{b}=r_{c}}
Jednake dužine
Jednake dužine imaju težišnice, visine bisektrise.
t
a
=
t
b
=
t
c
=
t
{\displaystyle t_{a}=t_{b}=t_{c}=t}
h
a
=
h
b
=
h
c
=
t
{\displaystyle h_{a}=h_{b}=h_{c}=t}
Značajne tačke trougla
Težište, ortocentar, centar opisanog i upisanog trougla se poklapaju.
Ovo su osobine koje su jedinstvene za jednakostraničan trougao.
R
r
=
a
3
3
6
a
=
6
3
=
2
{\displaystyle {\frac {R}{r}}={\frac {\frac {a}{\sqrt {3}}}{{\frac {\sqrt {3}}{6}}a}}={\frac {6}{3}}=2}
[2]
Odnos površine kružnice upisane u jednakostranični trougao i površine trougla je
3
a
2
π
36
a
2
3
4
=
12
a
2
π
36
a
2
3
=
π
3
3
{\displaystyle {\frac {\frac {3a^{2}\pi }{36}}{\frac {a^{2}{\sqrt {3}}}{4}}}={\frac {12a^{2}\pi }{36a^{2}{\sqrt {3}}}}={\frac {\pi }{3{\sqrt {3}}}}}
Odnos površine trougla i kvadrata njegovog obima
a
2
3
36
a
2
=
a
2
3
36
a
2
=
1
12
3
{\displaystyle {\frac {a^{2}{\sqrt {3}}}{36a^{2}}}={\frac {a^{2}{\sqrt {3}}}{36a^{2}}}={\frac {1}{12{\sqrt {3}}}}}
Ako su vrhovi
A
1
{\displaystyle A_{1}}
A
2
{\displaystyle A_{2}}
A
3
{\displaystyle A_{3}}
A
1
A
2
A
3
{\displaystyle A_{1}A_{2}A_{3}}
z
1
{\displaystyle z_{1}}
z
2
{\displaystyle z_{2}}
z
3
{\displaystyle z_{3}}
A
1
A
2
A
3
{\displaystyle A_{1}A_{2}A_{3}}
∣
z
1
−
z
2
∣=∣
z
2
−
z
3
∣=∣
z
3
−
z
1
∣
{\displaystyle \mid z_{1}-z_{2}\mid =\mid z_{2}-z_{3}\mid =\mid z_{3}-z_{1}\mid }
z
1
2
+
z
2
2
+
z
3
2
=
z
1
z
2
+
z
2
Z
3
+
z
3
z
1
{\displaystyle z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=z_{1}z_{2}+z_{2}Z_{3}+z_{3}z_{1}}
z
2
−
z
1
z
3
−
z
1
=
z
3
−
z
2
z
1
−
z
2
{\displaystyle {\frac {z_{2}-z_{1}}{z_{3}-z_{1}}}={\frac {z_{3}-z_{2}}{z_{1}-z_{2}}}}
1
z
−
z
1
=
1
z
−
z
2
=
1
z
−
z
3
{\displaystyle {\frac {1}{z-z_{1}}}={\frac {1}{z-z_{2}}}={\frac {1}{z-z_{3}}}}
z
=
z
−
1
+
z
2
+
z
3
3
{\displaystyle z={\frac {z-1+z_{2}+z_{3}}{3}}}
(
z
1
+
ϵ
z
2
+
ϵ
2
z
3
)
(
z
1
+
ϵ
2
z
2
+
ϵ
z
3
)
=
0
{\displaystyle (z_{1}+\epsilon z_{2}+\epsilon ^{2}z_{3})(z_{1}+\epsilon ^{2}z_{2}+\epsilon z_{3})=0}
ϵ
=
c
o
s
2
π
3
+
i
s
i
n
2
π
3
{\displaystyle \epsilon =cos{\frac {2\pi }{3}}+isin{\frac {2\pi }{3}}}
|
1
1
1
z
1
z
2
z
3
z
2
z
3
z
1
|
=
0
{\displaystyle {\begin{vmatrix}1&1&1\\z_{1}&z_{2}&z_{3}\\z_{2}&z_{3}&z_{1}\end{vmatrix}}=0}
Ako su
A
1
(
a
1
{\displaystyle A1(a_{1}}
A
2
(
a
2
)
{\displaystyle A_{2}(a_{2})}
A
3
(
a
3
)
{\displaystyle A_{3}(a_{3})}
A
1
A
2
A
3
{\displaystyle A_{1}A_{2}A_{3}}
A
1
A
2
A
3
{\displaystyle A_{1}A_{2}A_{3}}
z
3
−
z
1
=
ϵ
(
z
2
−
z
1
)
{\displaystyle z_{3}-z_{1}=\epsilon (z_{2}-z_{1})}
ϵ
=
c
o
s
π
3
+
i
s
i
n
π
3
{\displaystyle \epsilon =cos{\frac {\pi }{3}}+isin{\frac {\pi }{3}}}
z
2
−
z
1
=
ϵ
(
z
3
−
z
1
)
{\displaystyle z_{2}-z_{1}=\epsilon (z_{3}-z_{1})}
ϵ
=
c
o
s
5
π
3
+
i
s
i
n
5
π
3
{\displaystyle \epsilon =cos{\frac {5\pi }{3}}+isin{\frac {5\pi }{3}}}
z
1
+
ϵ
z
2
+
ϵ
2
z
3
=
0
{\displaystyle z_{1}+\epsilon z_{2}+\epsilon ^{2}z_{3}=0}
Za bilo koju tačku P u ravni trougla čije su udaljenosti
p
{\displaystyle p}
q
{\displaystyle q}
t
{\displaystyle t}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
3
(
p
4
+
q
4
+
t
4
+
a
4
)
=
(
p
2
+
q
2
+
t
2
+
a
2
)
2
{\displaystyle 3(p^{4}+q^{4}+t^{4}+a^{4})=(p^{2}+q^{2}+t^{2}+a^{2})^{2}}
Za bilo koju tačku
P
{\displaystyle P}
p
{\displaystyle p}
q
{\displaystyle q}
t
{\displaystyle t}
4
(
p
2
+
q
2
+
t
2
)
=
5
a
2
{\displaystyle 4(p^{2}+q^{2}+t^{2})=5a^{2}}
Konstrukcija
malo Povučemo pravu
Na njoj konstruišemo kružnicu čiji je prečnik jednak 2a.
Presječna tačka kružnice i prave je centar druge kružnice prečnika 2a.
Dobijene tačke kao presjek te dvije kružnice i njihov presjek sa pravom su vrhovi trougla
II način
Povučemo pravu i konstruišemo kružnicu prečnika 2a čiji je centar na pravoj.
presjek kružnice i prave je tačka koju uzmemo za centar kružnice istog prečnika.
Presjek te dvije kružnice su tačke čija udaljenost iznosi a. Sada lako dobijamo i treću tačku.
Izvođenje formule za površinu [ uredi | uredi izvor ] malo Formulu za površinu
P
=
3
4
a
2
{\displaystyle P={\frac {\sqrt {3}}{4}}a^{2}}
A
=
1
2
a
h
.
{\displaystyle A={\frac {1}{2}}ah.}
(
a
2
)
2
+
h
2
=
a
2
{\displaystyle \left({\frac {a}{2}}\right)^{2}+h^{2}=a^{2}}
h
=
3
2
a
.
{\displaystyle h={\frac {\sqrt {3}}{2}}a.}
P
=
3
4
a
2
.
{\displaystyle P={\frac {\sqrt {3}}{4}}a^{2}.}
P
=
1
2
a
b
sin
C
.
{\displaystyle P={\frac {1}{2}}ab\sin C.}
P
=
1
2
a
b
sin
60
∘
.
{\displaystyle P={\frac {1}{2}}ab\sin 60^{\circ }.}
P
=
1
2
a
b
×
3
2
=
3
4
a
b
=
3
4
a
2
{\displaystyle P={\frac {1}{2}}ab\times {\frac {\sqrt {3}}{2}}={\frac {\sqrt {3}}{4}}ab={\frac {\sqrt {3}}{4}}a^{2}}
Arheološko nalazište Lepenski Vir u Srbiji, iz doba neolita, sadrži ostatke staništa koja u svojoj osnovi imaju jednakostranični trougao.
Davidova zvijezda, simbol jevrejskog naroda, sastoji se od dva obrnuta jednakostranična trougla. Uz ove trouglove se povezuju i izvjesna religiozna značenja.
Mistični simbol Pitagorejaca, tetraktis, bio je oblika jednakostraničnog trougla.
Na zastavi Filipina
Oblik saobraćajnog znaka. Equilateral Triangle NEW PROOF OF EULER’S INRADIUS - CIRCUMRADIUS INEQUALITY Another Proof of the Erdos-Mordell Theorem Equilateral Triangles and Kiepert Perspectorsin Complex Numbers Non-Euclidean Versions of Some Classical Triangle Inequalities AN ELEMENTARY PROOF OF BLUNDON’S INEQUALITY Primene kompleksnih brojeva u geometriji 07.12.2011 [mrtav link 




















![{\displaystyle h={\frac {a\cdot {\sqrt[{}]{3}}}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49bcf3559d711d17a0cd881b98bb35c2c41b3e62)
![{\displaystyle P={\frac {h^{2}\cdot {\sqrt[{}]{3}}}{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a05bf2a9a83b87720ffe3e25719ad8545ba547be)
![{\displaystyle h={\sqrt[{}]{\frac {3P}{\sqrt[{}]{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39cd197d19853f9663986675b639ebd1e50b3141)
![{\displaystyle h={\sqrt[{}]{\frac {3P\,{\sqrt[{}]{3}}}{3}}}={\sqrt[{}]{{P}\,{\sqrt[{}]{3}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d960c0c0f50c866180ac74bdc184473c2f6c6630)





































































