Integral

Za druga značenja pojma Integral pogledajte čvor članak.

Integral od f(x) od a do b je površina iznad x-ose i ispod krive y = f(x), minus površina ispod x-ose i iznad krivulje, za x u intervalu [a,b].

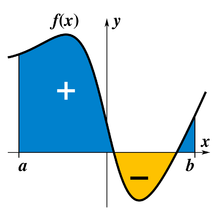
Integral je ključni koncept više matematike, unutar područja infinitezimalnog računa i matematičke analize. Za datu funkciju f(x) realne varijable x i interval [a,b] na pravcu realnih brojeva, integral

$\int_a^b f(x)dx$

predstavlja površinu područja u xy-ravni ograničenu grafikom od f, x-ose, i vertikalnim linijama x=a i x=b.

Ideju integrisanja su oblikovali u kasnom 17. vijeku Isaac Newton i Gottfried Wilhelm Leibniz. Zajedno s konceptom derivacije, integral je postao osnovni alat infinitezimalnog računa, s brojnim primjenama u nauci i inženjerstvu.

Jednu od prvih rigoroznih matematičkih definicija integrala dao je Bernhard Riemann. Zasnovana je na postupku određivanja granične vrijednosti (limesa), koji aproksimira površinu kurvilinearnog područja razbijanjem u vertikalne odsječke. Počevši od 19. vijeka, pojavljuju se složenije oznake integrisanja, pri čemu se poopćuje tip funkcije i domena integracije. Krivolinijski integral je definisan za funkcije dvije ili tri varijable, i interval integracije [a,b] je zamijenjen određenim krivima koje spajaju dvije točke ravni ili prostora. U površinskom integralu, kriva je zamijenjena dijelom površi trodimenzionalnog prostora. Integrali diferencijalnih formi igraju fundamentalnu ulogu u savremenoj diferencijalnoj geometriji. Ova su poopćenja integrala prvotno iznikla iz potreba fizike, i igraju značajnu ulogu u oblikovanju fizikalnih zakona, posebno u elektrodinamici. Apstraktnu matematičku teoriju poznatu kao Lebesque integracija je razvio Henri Lebesgue.

Naziv "integral" se također može odnositi sinonimno na značenje onoga od antiderivacije, funkcije F čija je derivacija data funkcija f. U ovom se slučaju zove neodređenim integralom, dok su integrali o kojima se raspravlja u ovom članku nazvani određenima. Osnovna teorema integralnog računa tvrdi da se antiderivacija može rabiti za računanje integrala nad intervalom. Neki autori, na primijer Tom Apostol, razlikuju antiderivaciju i neodređeni integral.

Također pogledajte

• Integro-diferencijalna jednačina

Vanjski linkovi

• Hazewinkel, Michiel, ed. (2001), "Integral", Matematička enciklopedija, Kluwer Academic Publishers, ISBN 978-1556080104 
• Riemann Sum by Wolfram Research
• Introduction to definite integrals by Khan Academy

Online knjige

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hussain, Faraz, Understanding Calculus, an online textbook
• Kowalk, W.P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) — a cookbook of definite integral techniques

Nedovršeni članak Integral koji govori o matematici treba dopuniti. Dopunite ga prema pravilima Wikipedije.